ルナハです。よろしくお願いします。では、さっそく始めていきましょう。
第3問
(4)次の論理関数Xは、ブール代数の公式等を利用して変形し、簡単にすると、(エ)になる。
手書き解説
ルナハノートを添付します↓
JPEGファイルも添付します↓
解説
正直、論理式の簡略化を解説するのは一番面倒ではありますなぜならゴチャゴチャしてくるからです。
これはブール代数の公式等が頭に入ってる+問題数を多く解いた方が試験本番でもうまくいきます。
あと少し運もあるでしょう(笑)私も得意ではないですね。
ここでは論理式の公理やブール代数の公式等の説明は省かせてもらいます。
MEMO
もし、公理やブール代数の公式等などがわかっていない方は「ブール代数 公式」で検索してみましょう。私なんかより詳しく丁寧なサイトがたくさんあります。では、解説をしていきます。
まず、問題のこの式を
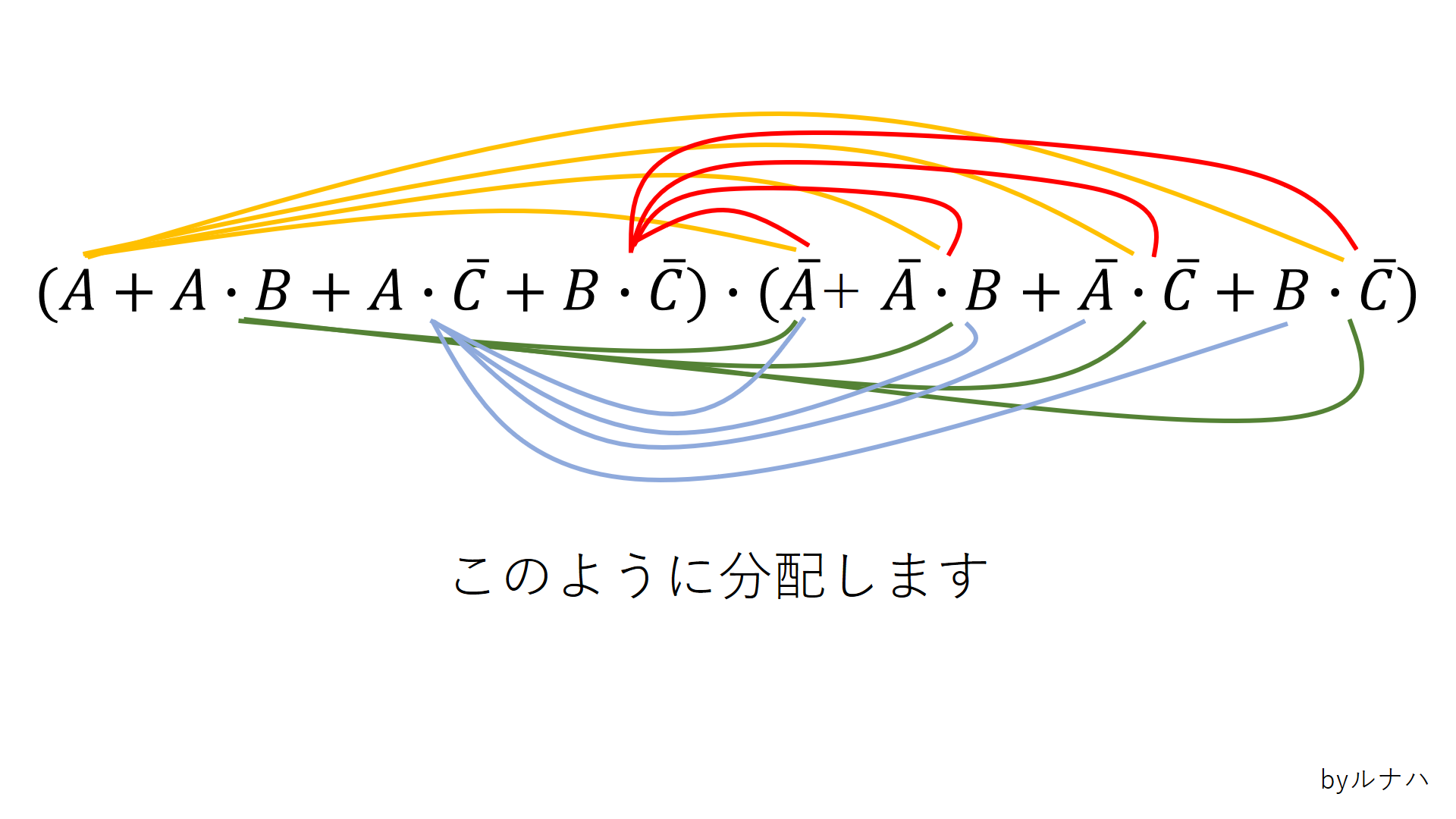
分配しますと、、、すこし見づらいですがこのようになります。↓
分配して計算すると、こうなります。
よって、答えは
となります。
今回使ったブール代数の基本定理を使用した順番に書いていきます。
- 分配の法則
- 恒等の法則、交換の法則
- 同一の法則
- 分配の法則
- 補元の法則
- 同一の法則
を使いました。
計算していくと答えが出ますよね。試験では結構時間が余る人も多いと思うので慌てないで解いて時間が余ったら確かめをよくしましょう。
(終)


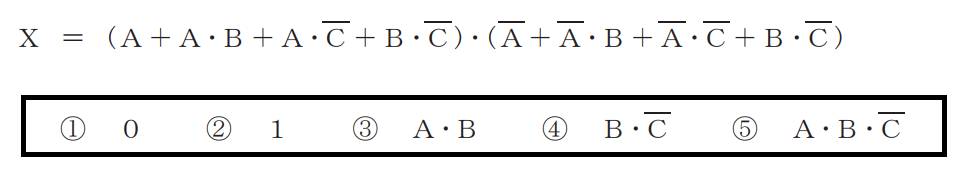

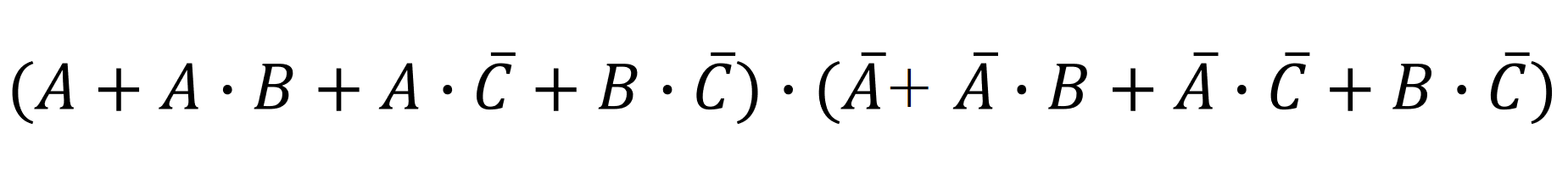
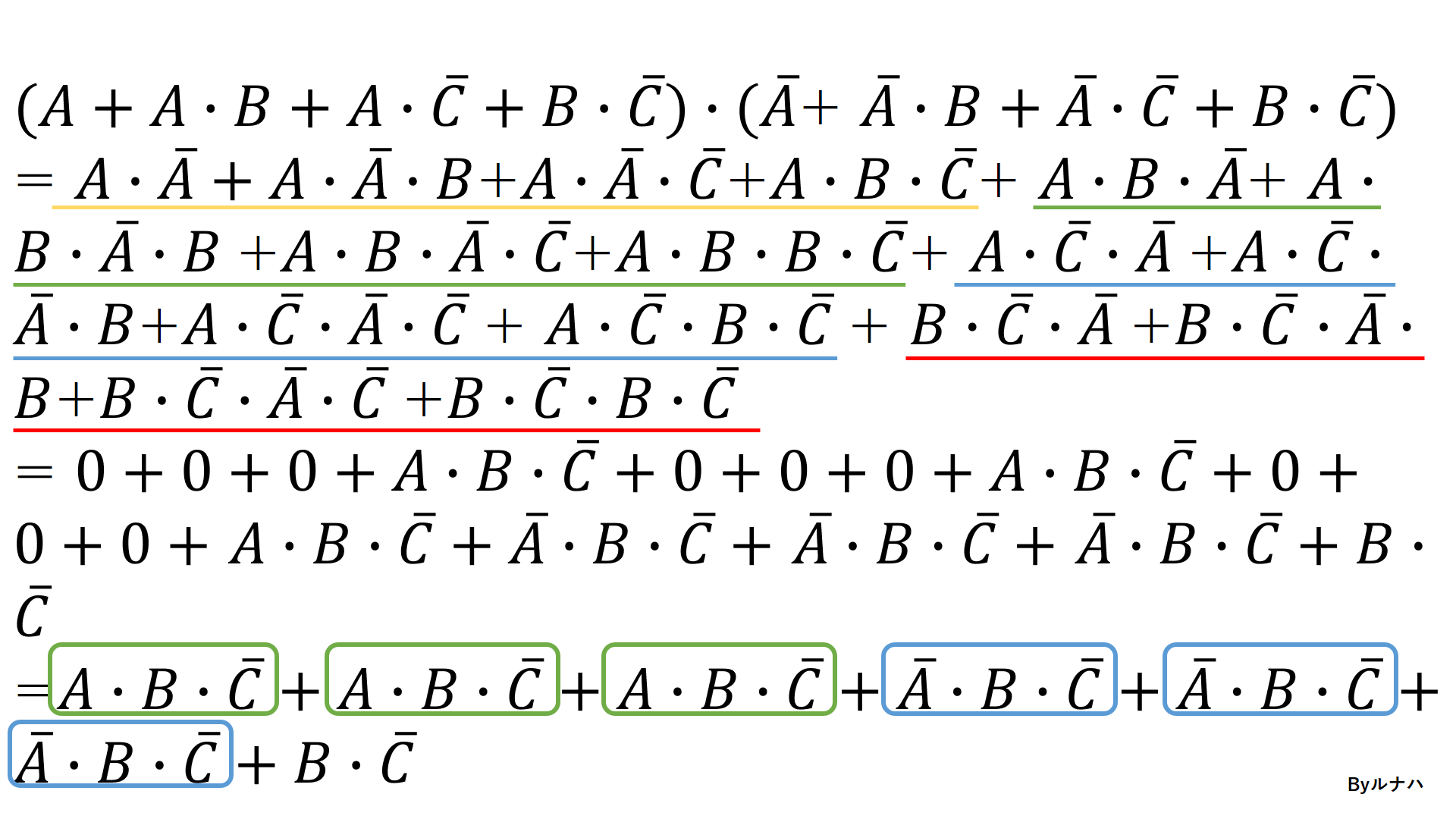



コメントを残す