ルナハです。よろしくお願いします。
第1問
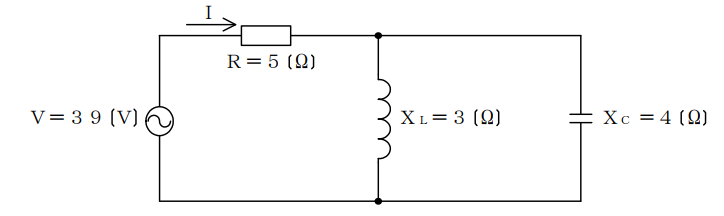
(2)図に示す回路において、抵抗Rに流れる電流Iは(イ)アンペアである。
手書き解説
以下にファイルを添付します。(毎度のこと手書きなのでご了承ください)↓
JPEGファイル↓
解説
今回の回路は抵抗Rは直列に接続されていますが、XLとXCは並列に接続されているのは見てわかります。
並列回路の合成抵抗を求める式は以下のようになる。
今回の問題も少し、このように抵抗と同じ考え方をする箇所があります。
しかし普通に並列の箇所を計算してから解くと失敗します。交流回路は直流より難しいといわれる所以はこの辺りにあります。
この条件を忘れないでください。
XL<XCの場合
リアクタンスXは
X=XC-XL
になります。大きさXは大きいほうから小さいほうを差し引くのでこのようになるのです。
しかし回路全体のインピーダンスZはXL>XCでもXL<XCでも変わらないです。
直列回路の場合の回路全体のインピーダンスZは以下になりますよね。
Z=√R^2+(XL-XC)^2
そうすると、今回の問題の場合の回路全体のインピーダンスZは以下になります。
あとは値を代入してI=V/Zで電流を求めます。
今回の回路の式は覚えておいたほうが良いでしょう。
ちなみにRLC並列回路になるとRも逆数の形になります。
計算するとZ=13[Ω]となります。
よってI=39/13=3[A]
答えは3[A]です。
(終)



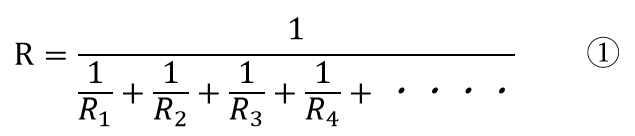
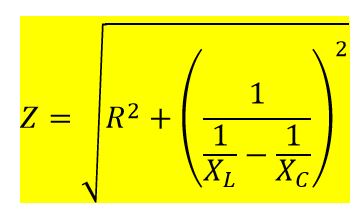


今回、5月27日に始めてDD2種を受けます。勉強するにあたりこちらのサイトでの解説は大変助かります。
ベン図の問題ですが、平成27年度問3の1問の解説をお願いできないでしょうか?論理和になるとイマイチ計算がわかりません。よろしくお願いします。
いつも当サイトを見ていただきありがとうございます(^_-)-☆
すみません、最近なかなか更新できずに目を通していませんでした。
今日が試験日ですね。良い報告待っています!
さて、もう遅いかもしれませんが一応、簡単に答えておきます。
平成27年度第2回のDD2種の第3問(1)は論理和ということで塗りつぶすとA・B以外は全部塗りつぶされていますよね。
そうなると全ての塗られた場合の論理式A+B+CからA・Bの部分を除いた形になります。
したがって、(A+B+C)notA・Bとなります。
論理積と論理和では求め方を臨機応変に対応していった方が良いと思います。
また工担は語群に論理式合わせないといけないのでそこのテクニックを身につけるともっと楽になります。
詳しくはまた解説を作っていく予定です。
質問ありがとうございました。