ルナハです。そろそろ近づいてきました。試験まで頑張っていきましょう。
第3問
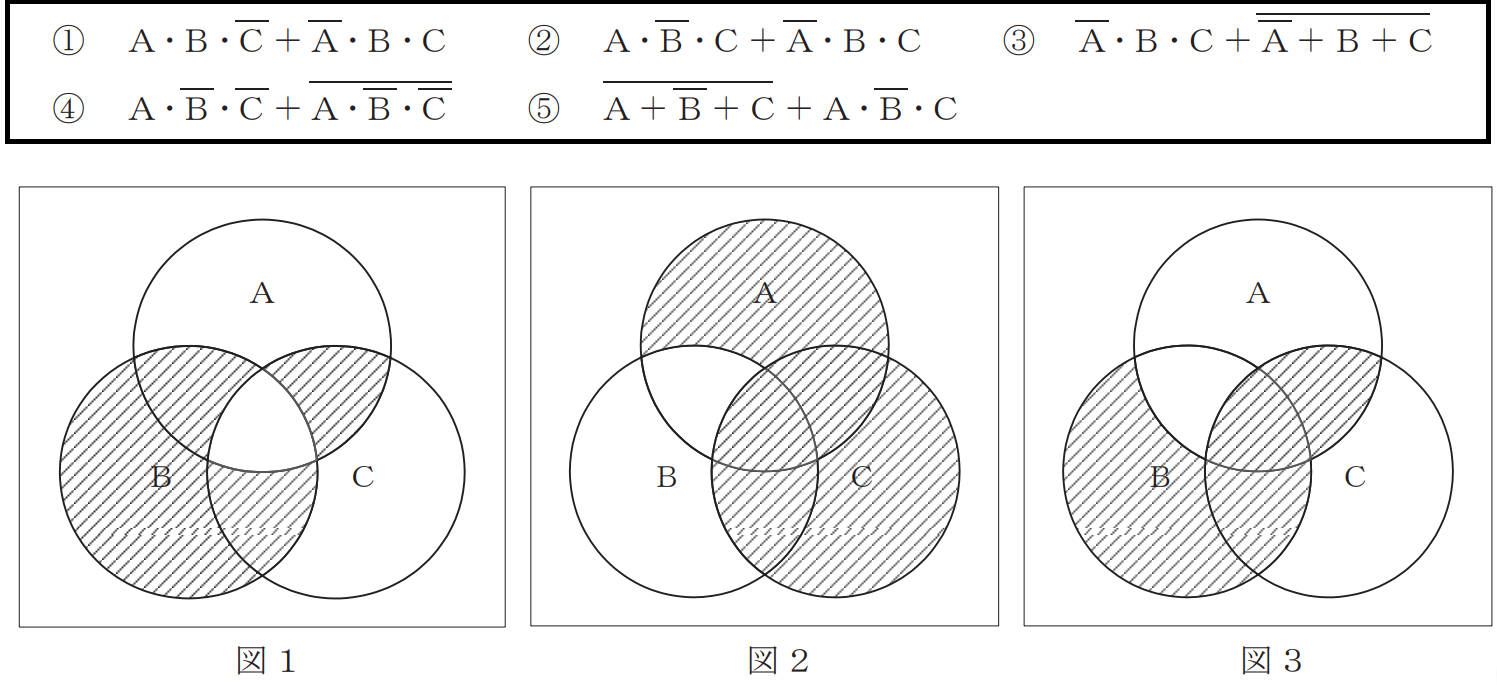
(1)図1、図2及び図3に示すベン図において、A、B及びCが、それぞれの円の内部を表すとき、図1、図2及び図3の斜線部分を示すそれぞれの論理式の論理積は、(ア)と表すことができる。
手書き解説
ルナハノートを添付します↓
JPEGファイルも添付します↓
解説
今回、初めて論理式のベン図について解説します。
まず、ベン図は問題の図1、図2及び図3を見てわかる通り工事担任者の問題では3つのベン図が重なっているものしか出題されません。このようなベン図の問題は実際とても簡単です。
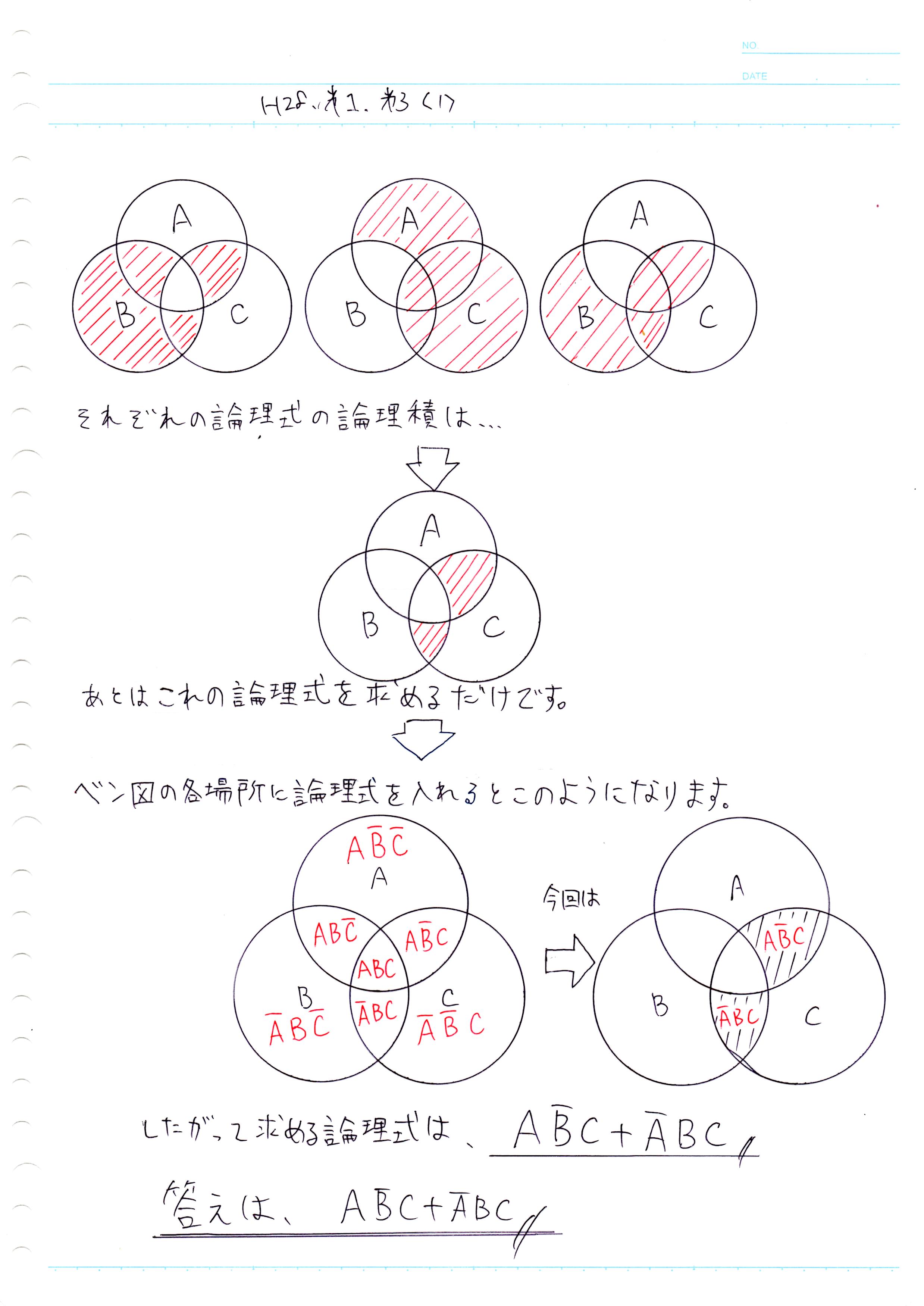
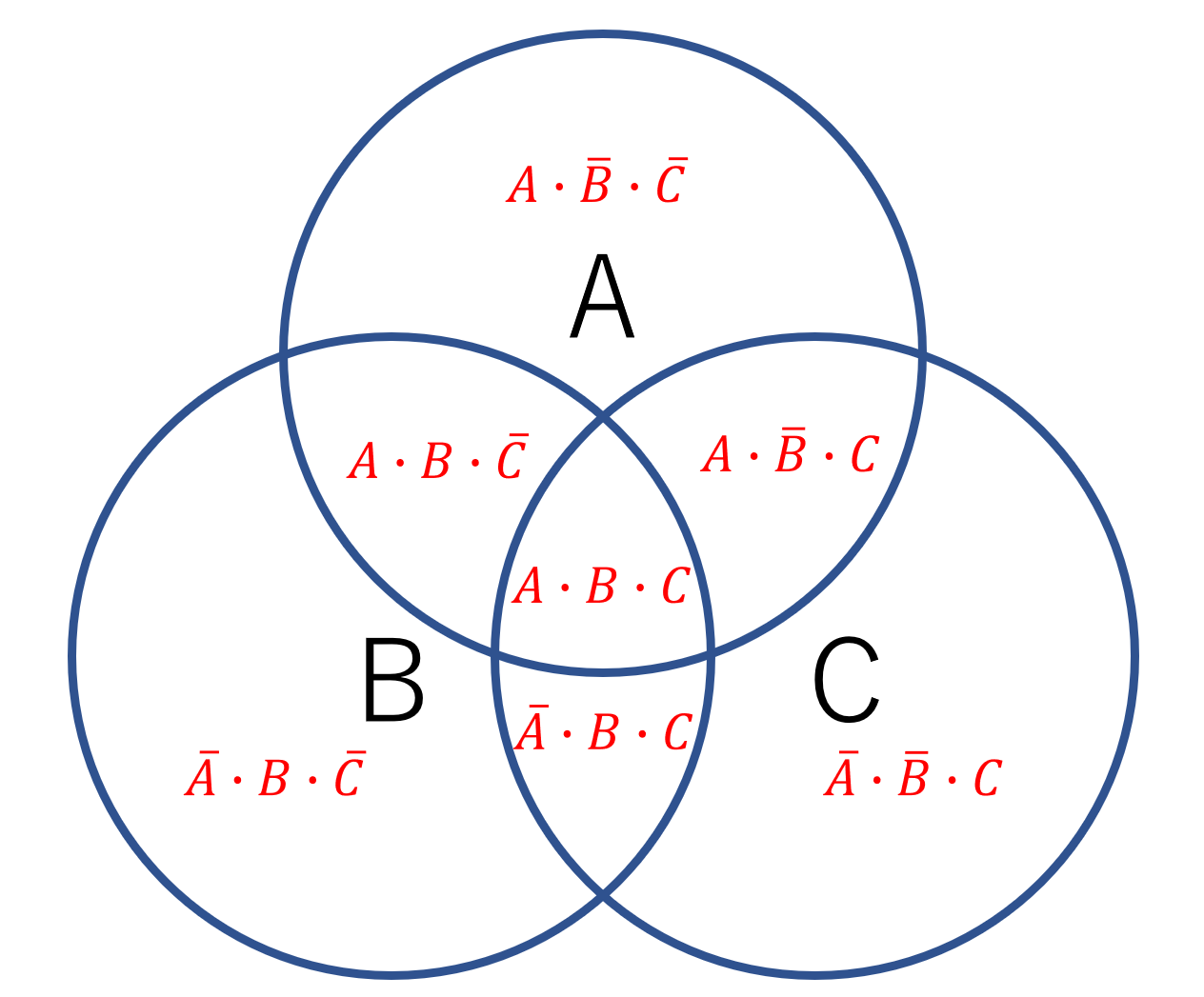
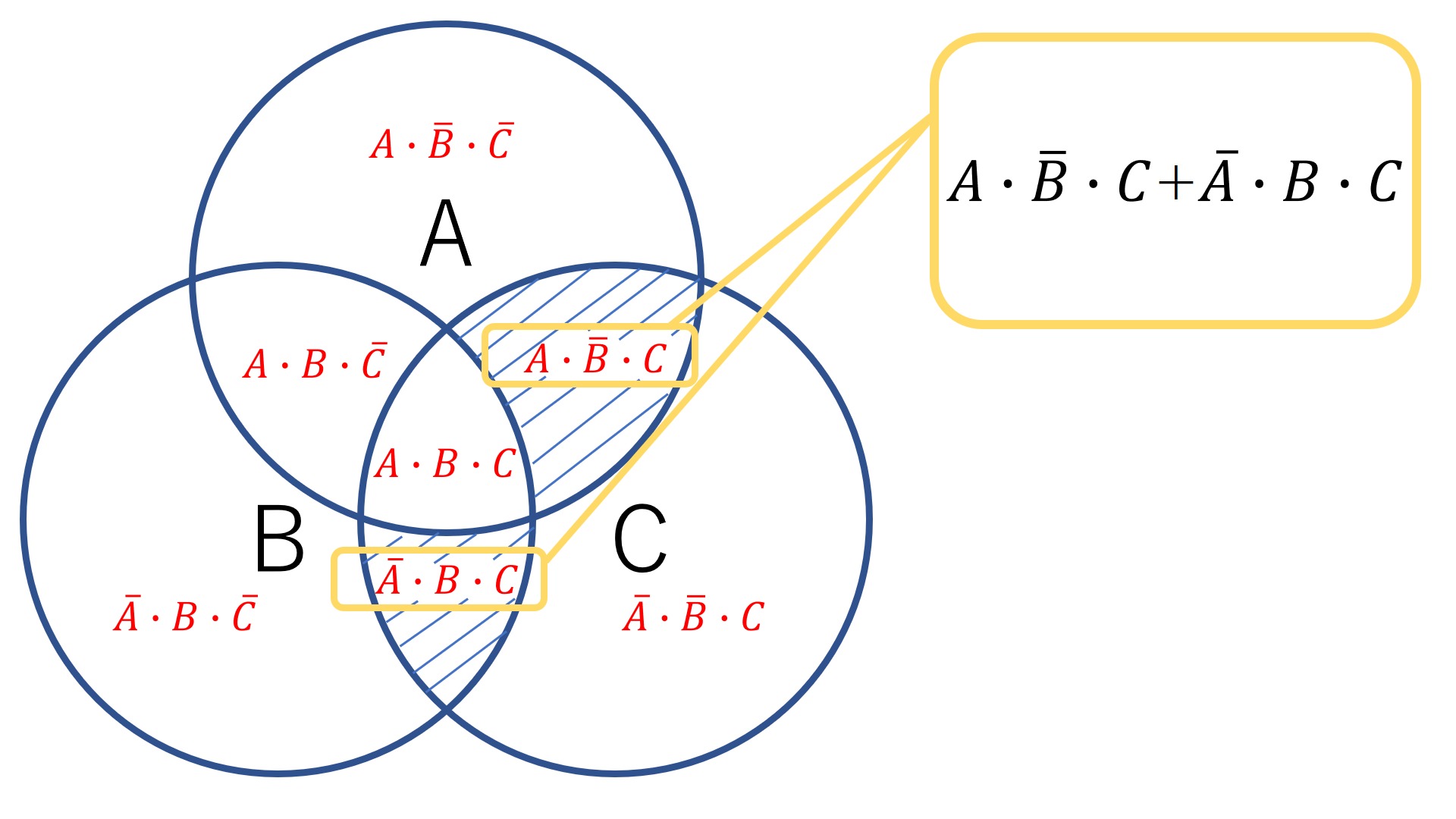
このようにベン図の各部分には以下のような論理式があります
図1-1のベン図の論理式は常に変わらないので毎回出題されるベン図の斜線を引かれている場所を読み取り論理式を足していけば終わりです。
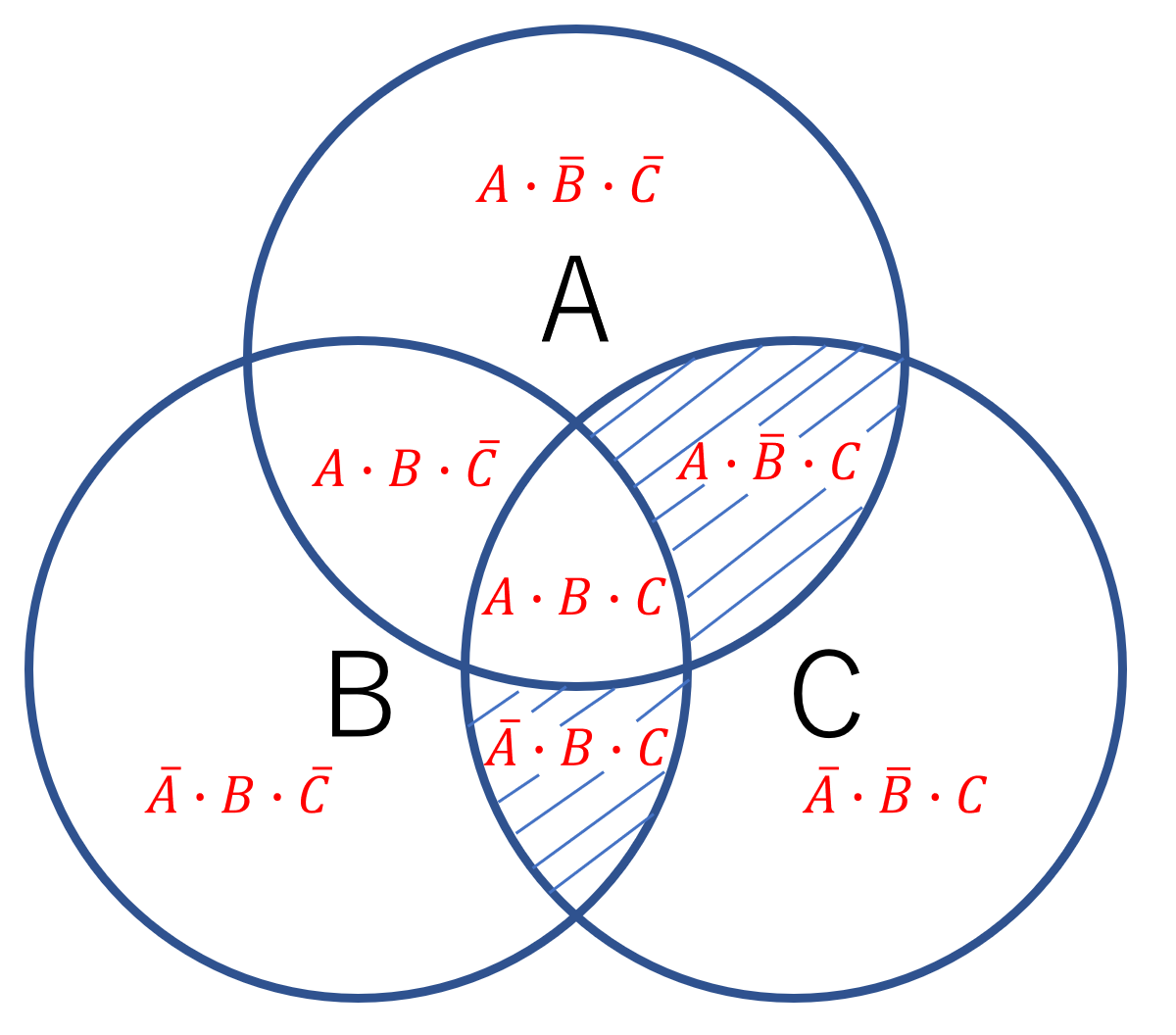
今回の問題は図1、図2及び図3のベン図の論理積ということなので、図1-1は次のように斜線が引けます。
ここまで出来たらあとはこの二つの論理式を足して終わりです。
以下のようにまとめます↓
よって答えは
となります。(終)
今回の問題は論理積なので、斜線が少なくて結果二個の論理式を足すだけで済みました。論理和のときは斜線の部分が多くなるので少し大変になりますがこの方法をを理解しておけば簡単にできますので是非参考にしてみてください。
論理回路は各問5点なので絶対抑えましょう。


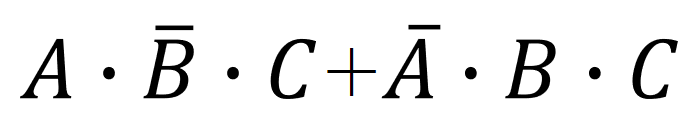


コメントを残す