ルナハです。よろしくお願いします。
問題を解説するにあたってカルノー図というものも使えますがカルノー図についてはまた今度説明しますので今回はブール代数を使い解説を行っていきます。ただし、別解として私がカルノー図で解いたのも載せておくので余裕がある方は見ていってください。
第3問
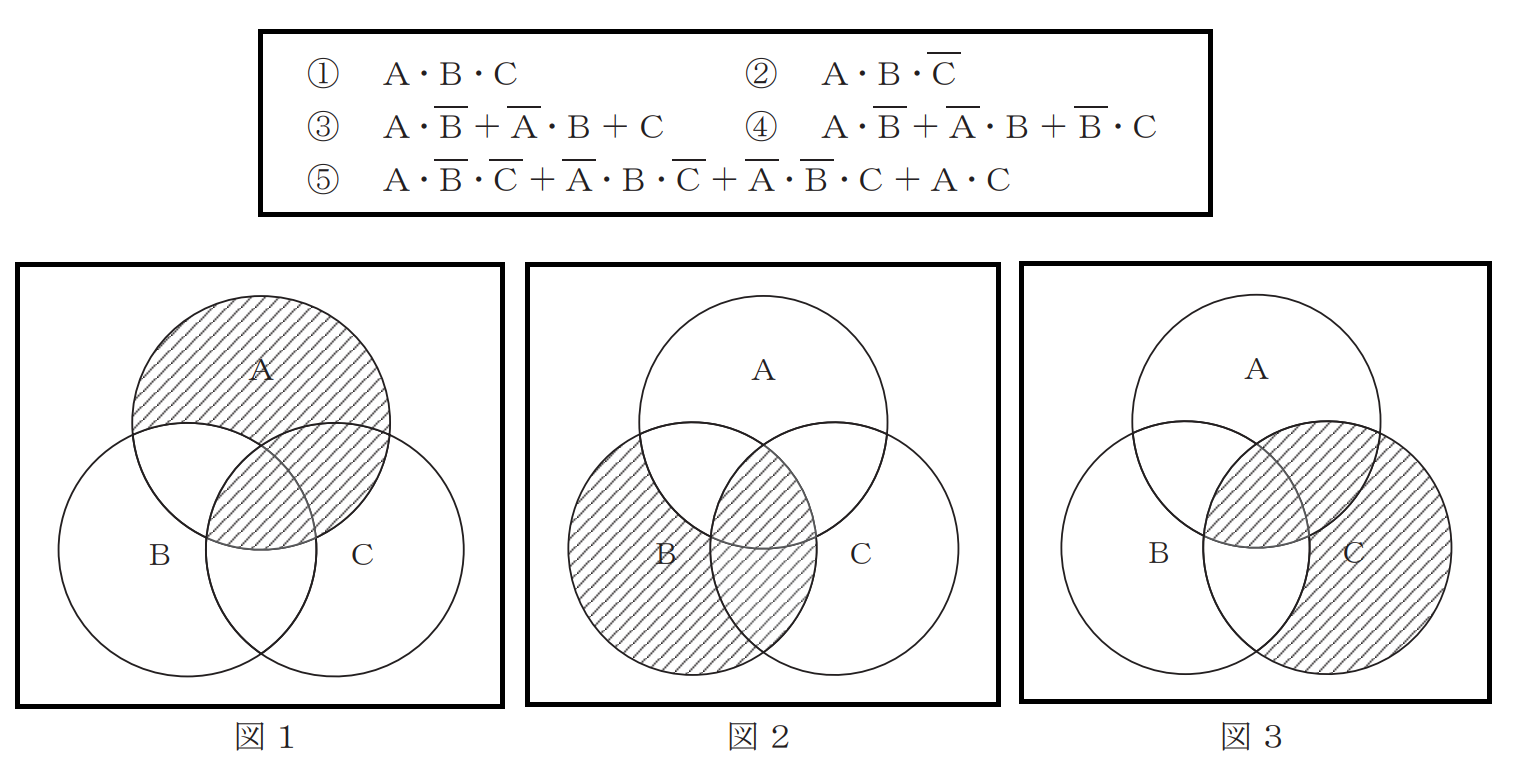
(1)図1、図2及び図3に示すベン図において、A、B及びCが、それぞれの円の内部を表すとき、図1、図2及び図3の斜線部分を示すそれぞれの論理式の論理和は、(ア)と表すことができる。
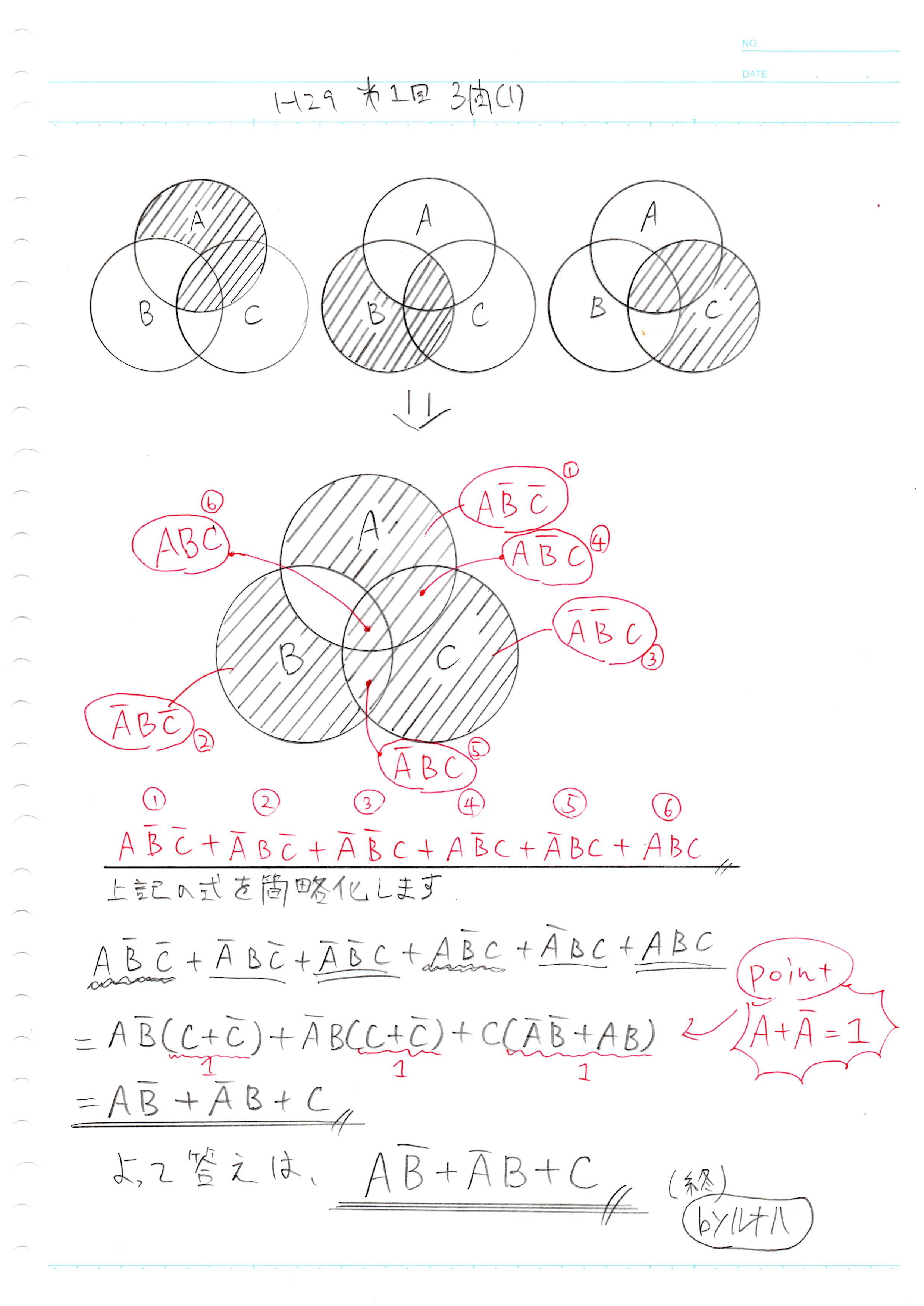
手書き解説
ルナハノートを添付します↓
JPEGファイルも添付します↓
解説
前も同じような問題もやりました。そのときは論理積でしたが今回は論理和なので斜線部分が多いですね。
類似問題↓
 【過去問 解説】工事担任者合格までの道のり~平成28年度第1回AI・DD総合種 基礎「第3問(1)」~
【過去問 解説】工事担任者合格までの道のり~平成28年度第1回AI・DD総合種 基礎「第3問(1)」~では早速ですが、解説をしていきます。
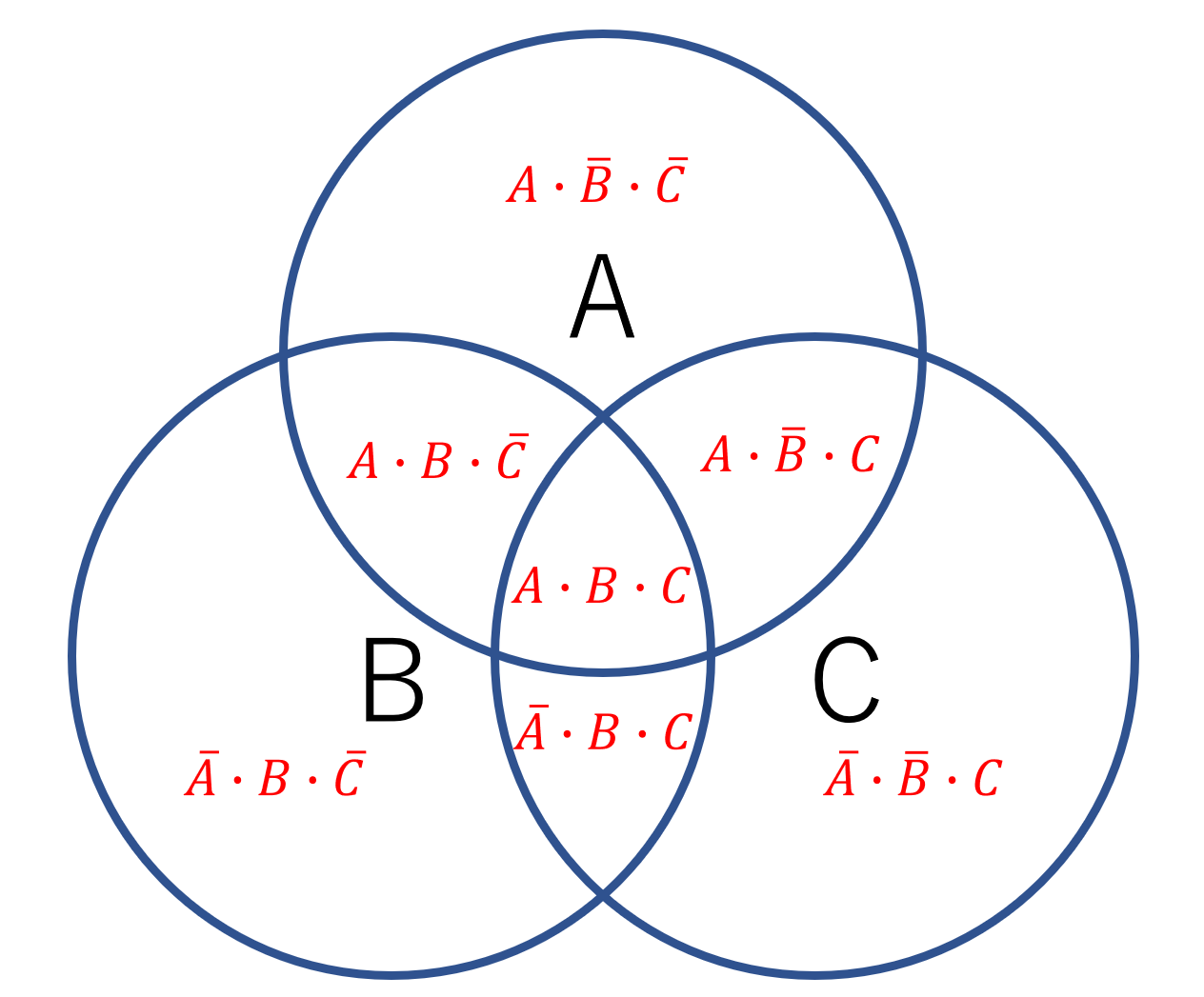
このようにベン図の各部分には以下のような論理式を書けます。
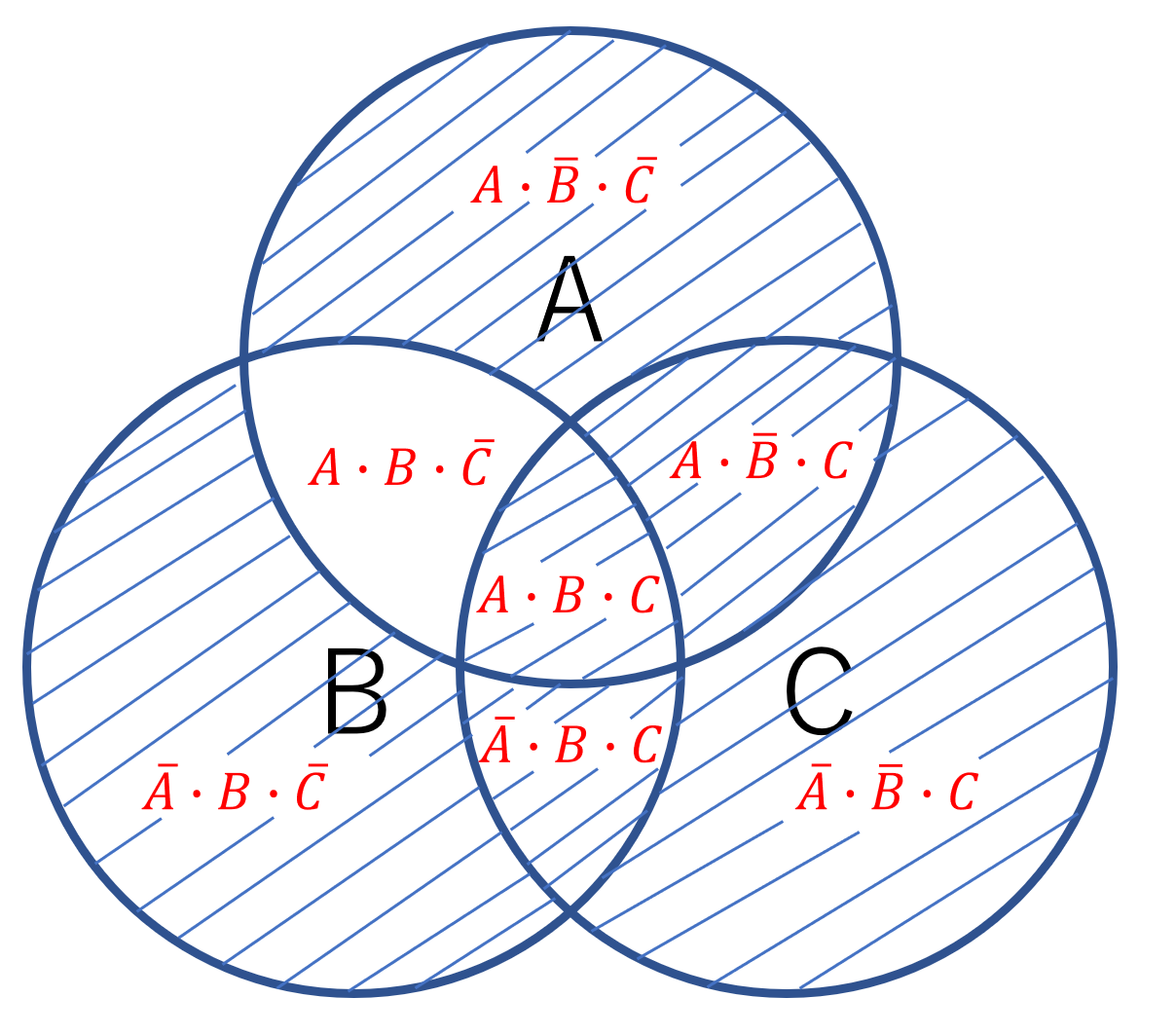
図1、図2及び図3の斜線部分の論理式の論理和ということなので、図1-1は図1-2のように斜線が引かれます。
斜線部分の論理式をすべて足してください。一つの長い論理式を作ります。
前の問題と違って斜線部分が多いうえにただ単に斜線の部分の論理式を足しても語群にはありません。
ここで、図1-3の論理式を簡単化する必要があります。
ブール代数を使い論理式を簡単化しますと以下のようになります。
ここまで簡単化すると語群と同じ論理式になりますよね。
よって、答えは
になります。
別解(カルノー図を利用する場合)
別解として論理式の簡略化をする際にカルノー図を用いて解く場合もあります。
一部カルノー図を使い解いたものを記します。参考まで見てみてください。詳しくはまたの機会にカルノー図を説明します。
まず第一に今回の論理和にしたときのベン図はこうなりますよね。
そこからさらに
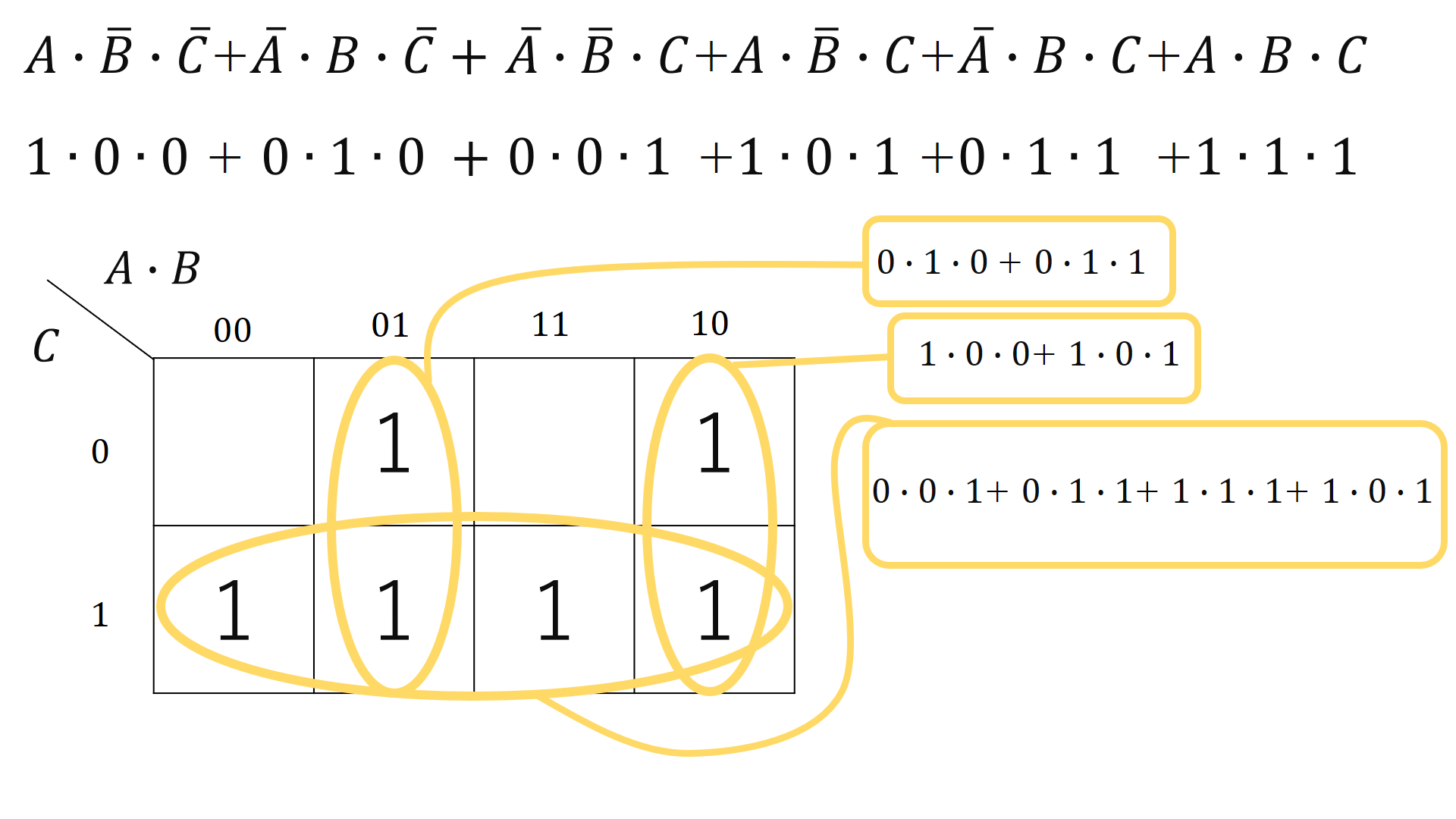
各斜線部分の論理式を足していき長い論理式を導きます。ここまでは先ほどの解説と同じ要領です。
ここの簡単化をカルノー図を使いますと、、、
このようになります。さらにカルノー図の解き方に沿っていくと、、
このようにカルノー図を用いて論理式を簡略化するのも慣れれば簡単です。一度試してみましょう。意外と論理回路自体自分で2、3問解いてみて慣れれば誰でも出来るようになります。根気よく頑張ってみましょう!
(終)byルナハ



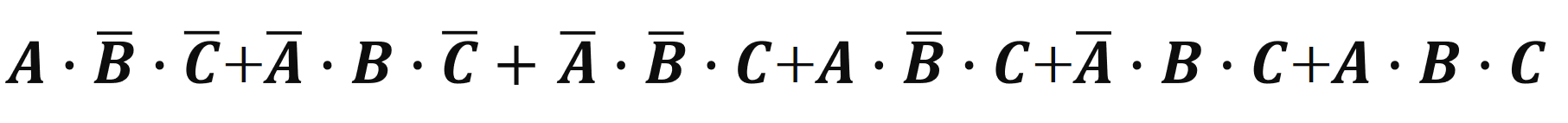
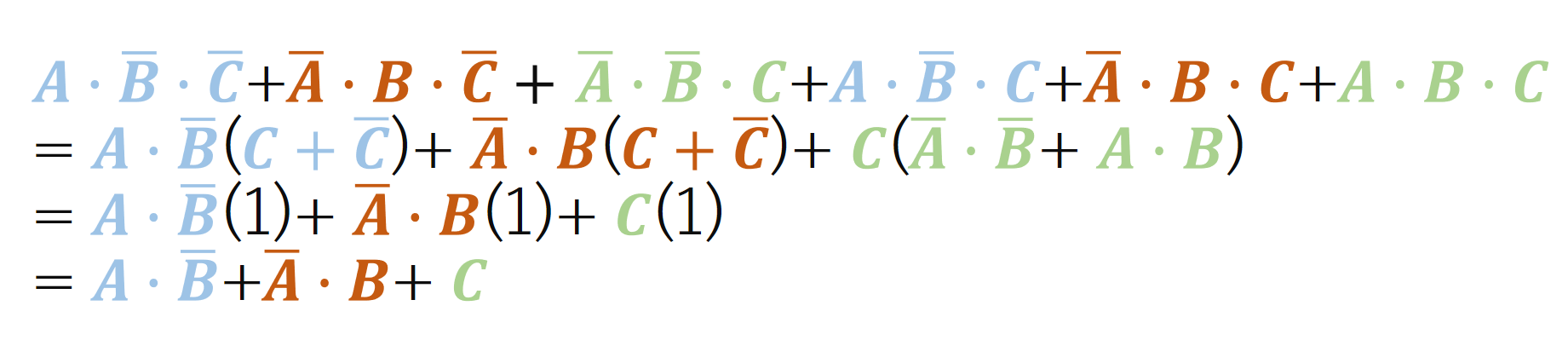
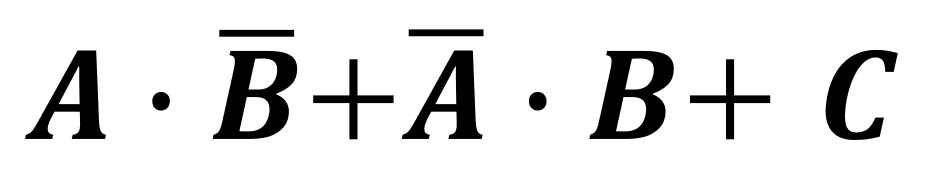



コメントを残す