【過去問 解説】工事担任者合格までの道のり～平成26年度第１回ＡＩ・ＤＤ総合種 基礎「第１問（２）」～

ルナハです。よろしくお願いします。

第２問

（２）図に示す回路において、端子a-b間に正弦波の交流電圧１４４ボルトを加えた場合、力率（抵抗Rに流れる電流IRと回路に流れる全電流Iとの比）が０．８であるとき、容量性リアクタンスXCは、（イ）オームである。

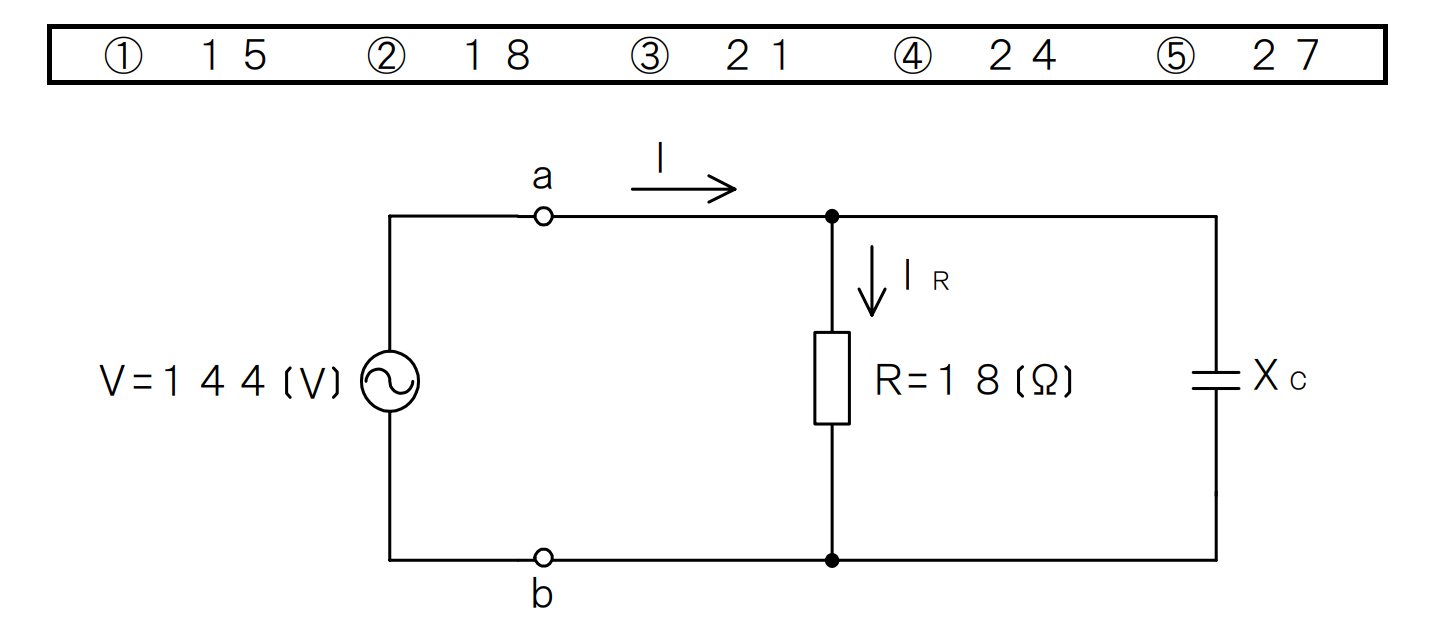
手書き解説

ルナハノートを添付します

平成26年度第１回総合種第１問（２）

ＪＰＥＧファイルも添付します↓

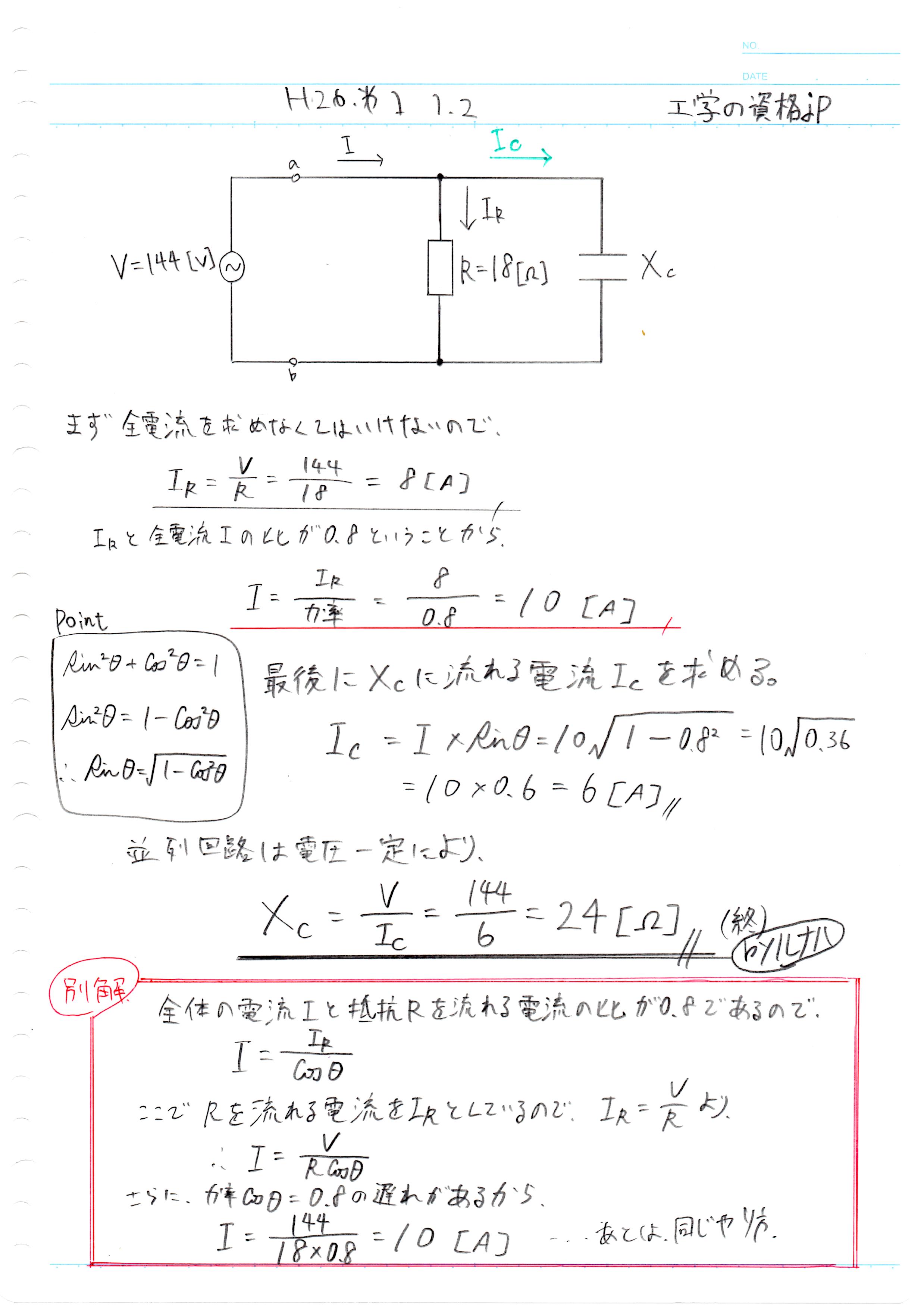
解説

まずは、問題で与えられているものを書き出します。

• 交流電圧V＝１４４
• 力率＝０．８
• 抵抗R＝１８

ですね。当たり前ですがこの与えられているものからXCを求めなくてはいけませんよね。

電気回路に限ったことではなく大体の問題は既知の数値から計算して出していきますから。

では、解説していきます。

まず、並列回路の場合は電圧は一定なので

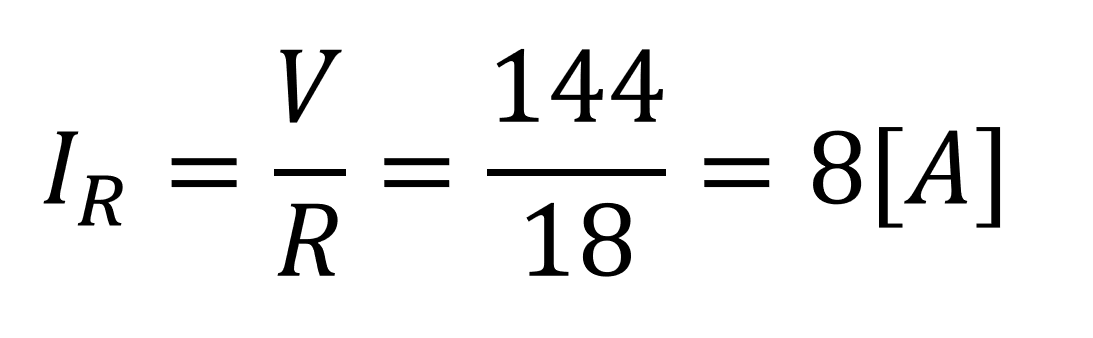
となります。

次に力率に注目します。

今求めた電流IRと全電流Iの比が０．８ということから全電流Iを求めると

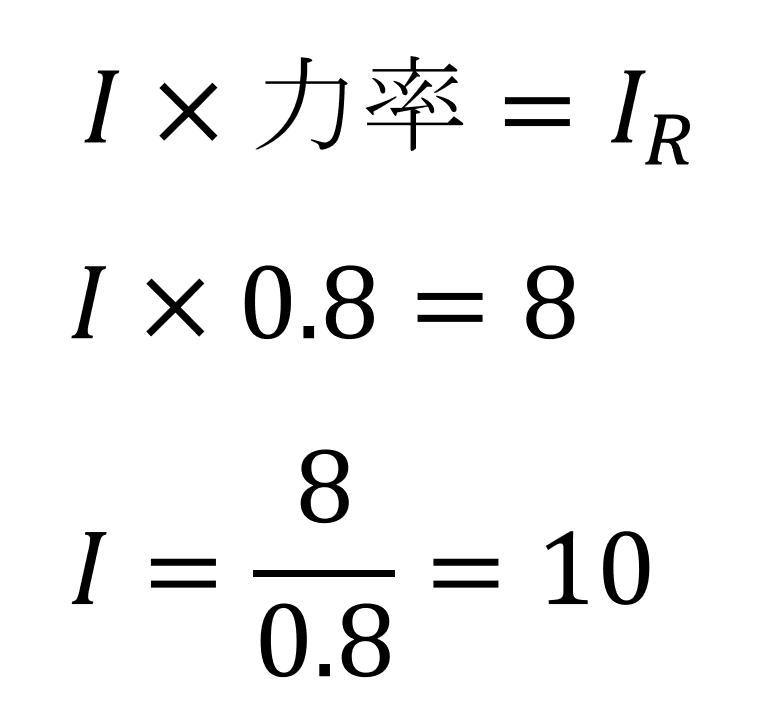
となります。

これによって全電流Iが求まりました。

ところで，三角関数の相互関係により以下のような式が求まります。

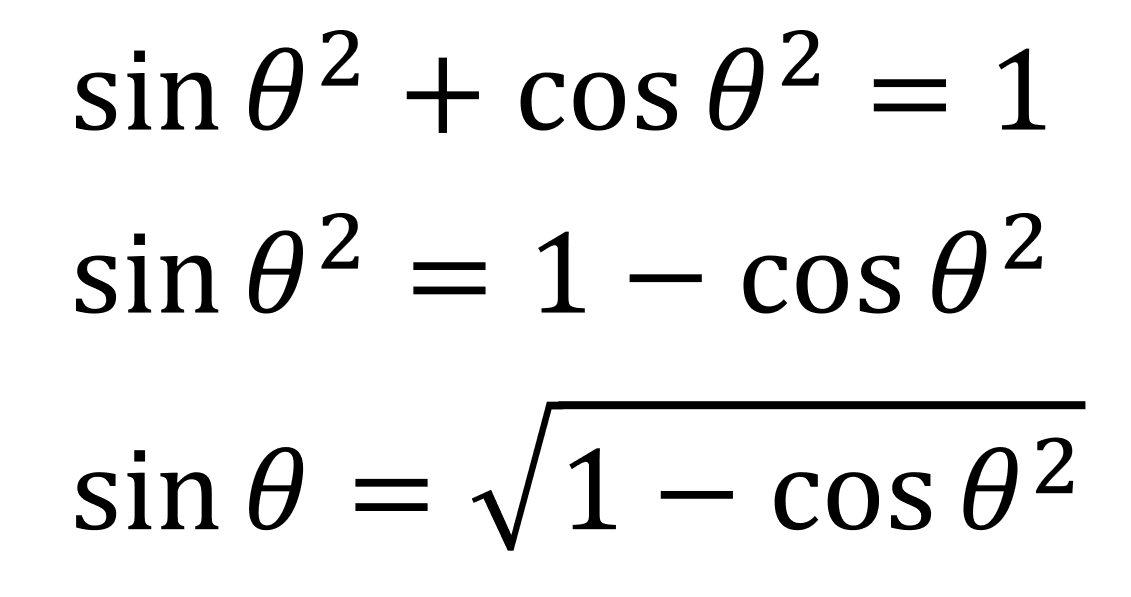
まぁ、これは数学の範囲内なので覚えるも良し、三平方の定理、三角関数の勉強するのも良しです！

抵抗Rに力率cosΘ＝０．８かかったとき、容量性リアクタンスにかかるsinΘは

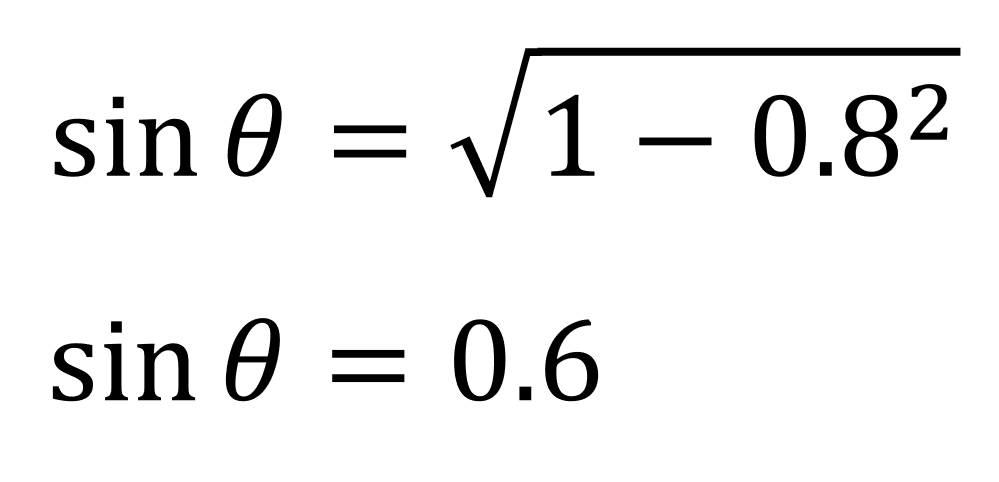
となります。

次に、容量性リアクタンスXCに流れる電流をICとすると、

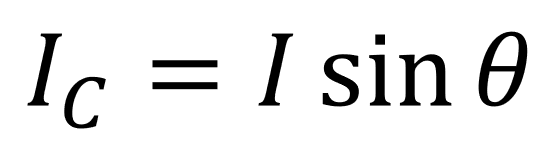
という式が成り立ちます。（sinΘに電気工学上の命名はされていない）

値を代入し計算すると

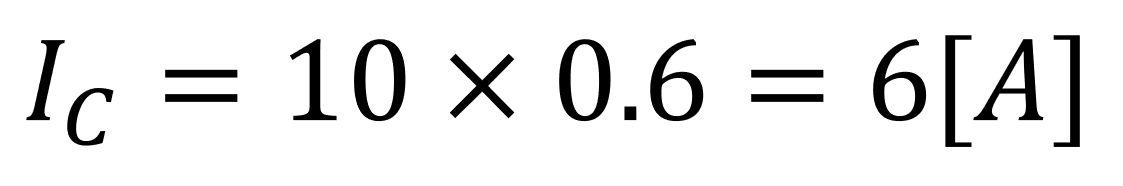
これで、容量性リアクタンスXCに流れる電流が求まりました。

最後に、容量性リアクタンスXC自体を求めます。

もう簡単に求まるはずです。

回路は並列回路なので、流れる電圧は一定です。あとはオームの法則より

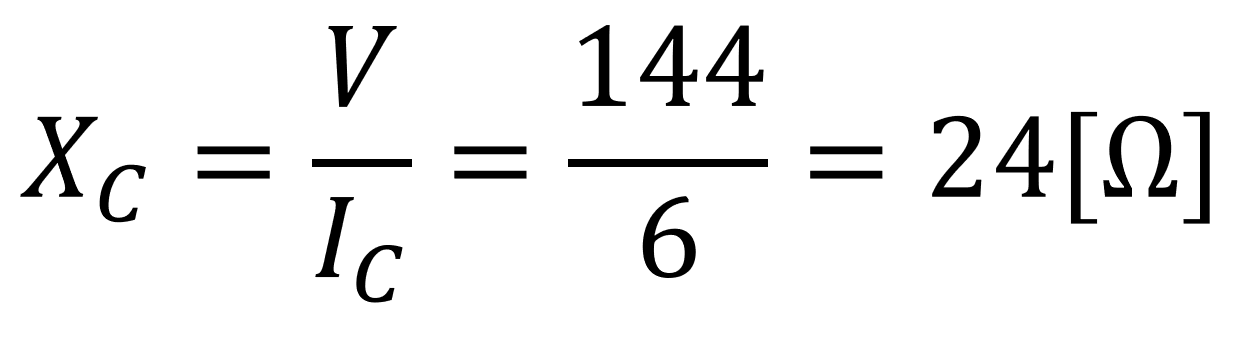
となります。

よって答えは２４オームです。

（終）

別解

全電流Iと抵抗Rに流れる電流IRの比が０．８であるので、

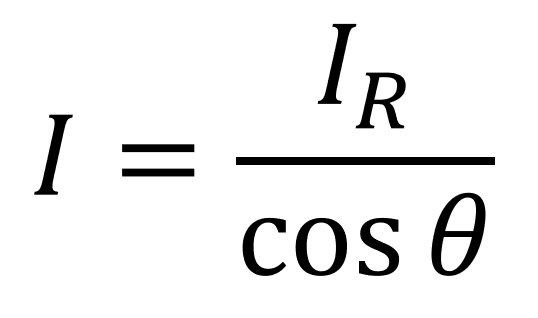
という式が求まります。

ここで抵抗Rに流れる電流IRはオームの法則、並列接続の場合電圧は一定より

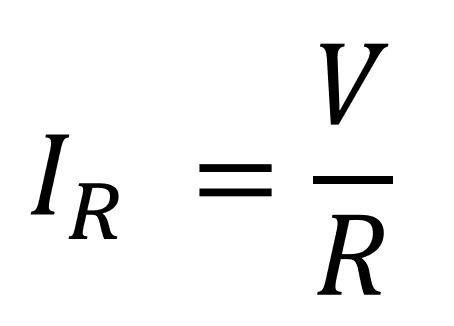
となり、全電流Iに代入すると

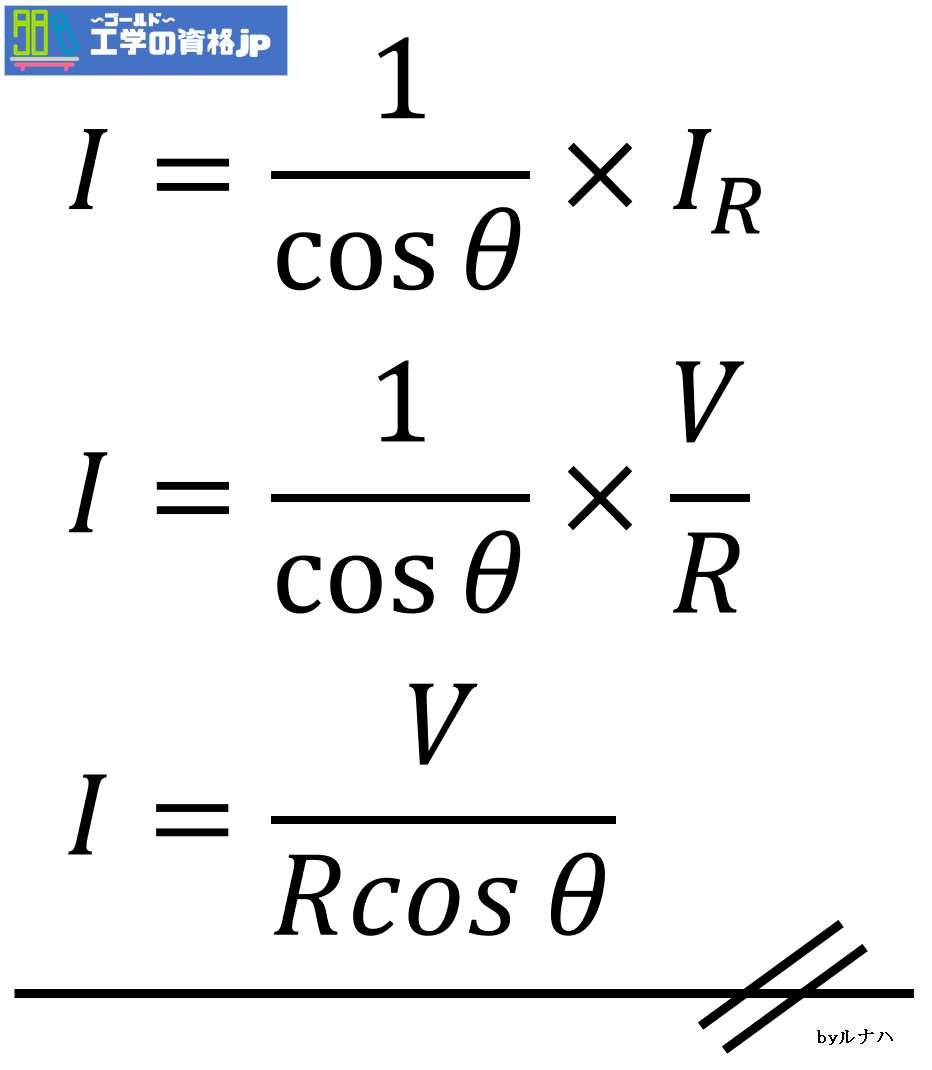
• 力率cosΘ＝０．８
• 抵抗R＝１８
• V＝１４４

を代入すると

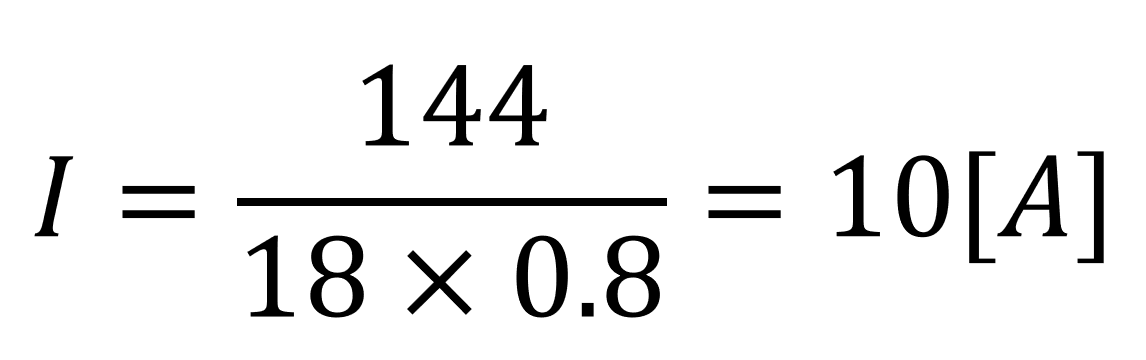
これで全電流Iが求まりました。

あとの計算は本解説と同じです。

（終）