ルナハです。宜しくお願いします。
今回から計算問題ではない問題もやっていこうと思います。
計算問題では無いのでいつものルナハノート(PDF)は無しでやっていこうと思います。
第1問
(3)コイルに交流電流が流れると、コイル内には時間的に変化する磁束が生じ、流れる電流を妨げる向きに誘導起電力が生ずる。このとき、コイルの自己インダクタンスは(ウ)で表される。

解説
では、はじめていきます。
まず大事な前提としてコイルに電流を流すと磁束が発生するというのは理解してください。
発生した磁束はコイル面も貫きます。磁束が変化するとコイルに誘導起電力が生じ,その結果電流が流れます。
このように、回路を流れる電流が変化したとき自己の回路に誘導起電力を生じる現象を自己誘導と言います。この誘導起電力の大きさは、時間当たりに磁束が変化する割合すなわち電流が変化する割合に比例し、さらに自己インダクタンスL[H]に比例する。
ここで自己インダクタンスを表すために必要なものを以下に記します。

すなわち、自己誘導により生じる誘導起電力の大きさをe[V]は、
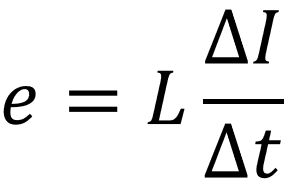
となります。
MEMO
e=Ziというオームの法則がここでも出るということですね。コイル、コンデンサ及び抵抗はZと見れます。電流Iはただ時間で変化しているから記述が変わっていますが、実際はただの電流Iです。電磁気と電気回路の分野でもこの関係は変わらないです。自己インダクタンスはこの式を変形して、次にように表される。(式変形も記します)
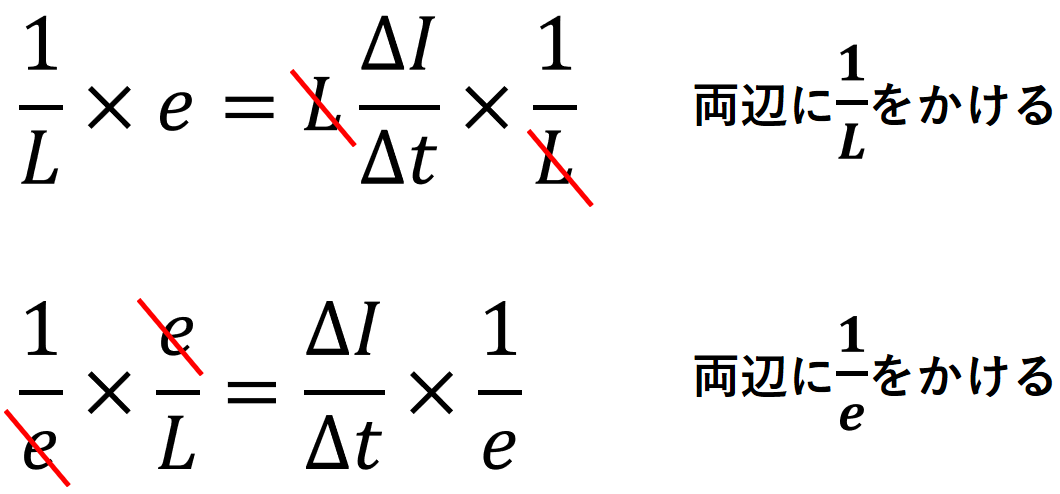
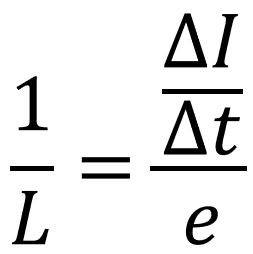
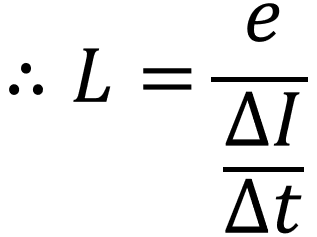
上記の自己インダクタンスLの式を先ほど表した文字で表現すると、

となります。
MEMO
ここでもZ=V/Iというオームの法則が成り立っていますね。問題を解くうえではまずL=V/Iの語群に注目してください。そうなると語群の③か④しかなくなります。最悪の場合でも50%の確率になりますよね。選択式の問題は単位など基本的なことから注目していきましょう。よって答えは誘導起電力/電流変化率となります。(終)



コメントを残す