第1問
(1)図に示す回路において、抵抗Rが(ア)オームであるとき、この抵抗Rに流れる電流は、3アンペアである。ただし、電池の内部抵抗は無視するものとする。
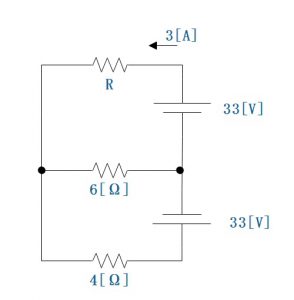
このような問題が出題されていました。
では、さっそく問題を解いていきたいと思います。
手書き解説
ここからは手書きなのでご了承ください。
下記に貼っておきます。
手書きでは汚くて申し訳ないので出来るところまでは記述します。
解説
この問題ではキルヒホッフの法則を大活用するのでここでしっかりと抑えましょう。
まず、6Ωの抵抗に流れる電流をIとします。これは任意ですのでなんでもいいですが。
電流は起電力の長いほうから流れますので二つの閉路内の上部は半時計回りです。
逆に下部の閉路は時計回りです。
そこで回路全体を見てみますと電流が問題に3[A]と書かれています。6Ωに流れる電流がIなので4Ωに流れる電流は3-I[A]となります。これはキルヒホッフの一つです。
川の流れとおなじですよね。もともと一つの川が二つに分かれてそのあと合流したらおなじ水の量ですからね。
そこまで理解したら二つの閉路の回路方程式を立てましょう。
ここでまたキルヒホッフの法則二つ目です。
起電力の向きと電流の向きに注意しながら連立方程式を立てます。
その前にオームの法則の
V=IR
を覚えましょう!今回はこの形で式を作ります。
イメージとしては、起電力の向きと電流の向きが同じならプラスです。
逆らってお互いがぶつかり合うならマイナスになります。
といことは上部の閉路は反時計回りで電流が来ているので3R(IR)と6I(RI)となります。
電圧が33Vなので
33=3R+6I ①
一つ出ます。
次に下部の式は時計回りなので起電力、電流の向きをしっかりとみて3-I[A]が4Ωとぶつかり合う関係にありますので、-4×(3-I)となります。これもよく見るとRIの関係にありますよね。さらに6Iが出ます。
電圧は33Vなので
33=-4×(3ーI)+6I ②
この二つを計算して
I=4.5[A]
を得る。
よってR=2[Ω]が求まります。
もしこの二つの式からの導出がわからない方がいるなら方程式の練習をしてから行ってください。
このように工事担任者の基礎第一問(1)は電気回路です。時間は少しかかるかもしれませんが練習すれば解けるようになります。
では、また次の解説で。
(終)




コメントを残す