ルナハです。宜しくお願いします。
第3問
(2)図に示す論理回路において、Mの論理素子が(イ)であるとき、入力A及び入力Bから出力Cの論理式を求め変形し、簡単にすると、![]() で表される。
で表される。
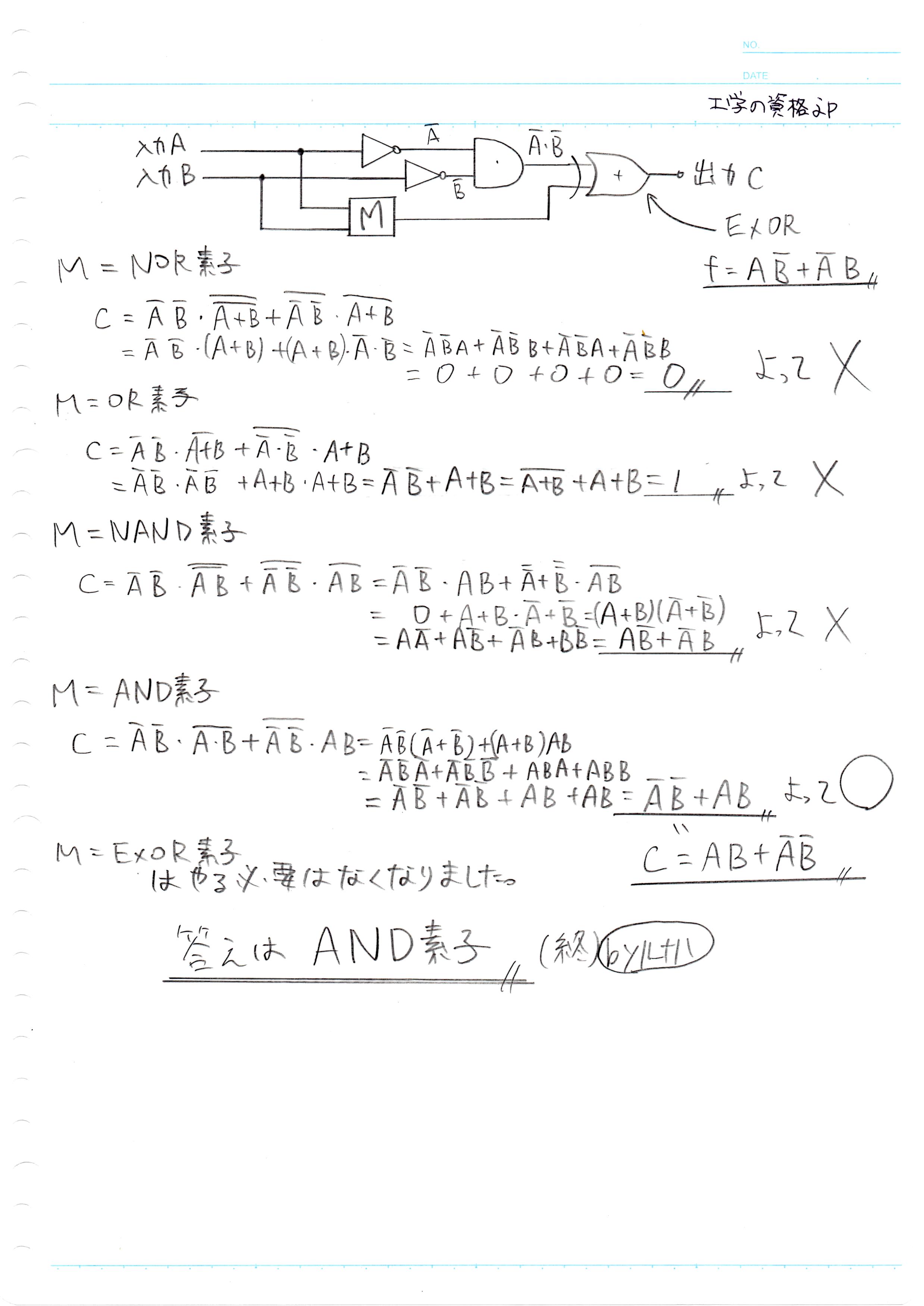
手書き解説
ルナハノートを添付します
JPEGファイルも添付します↓
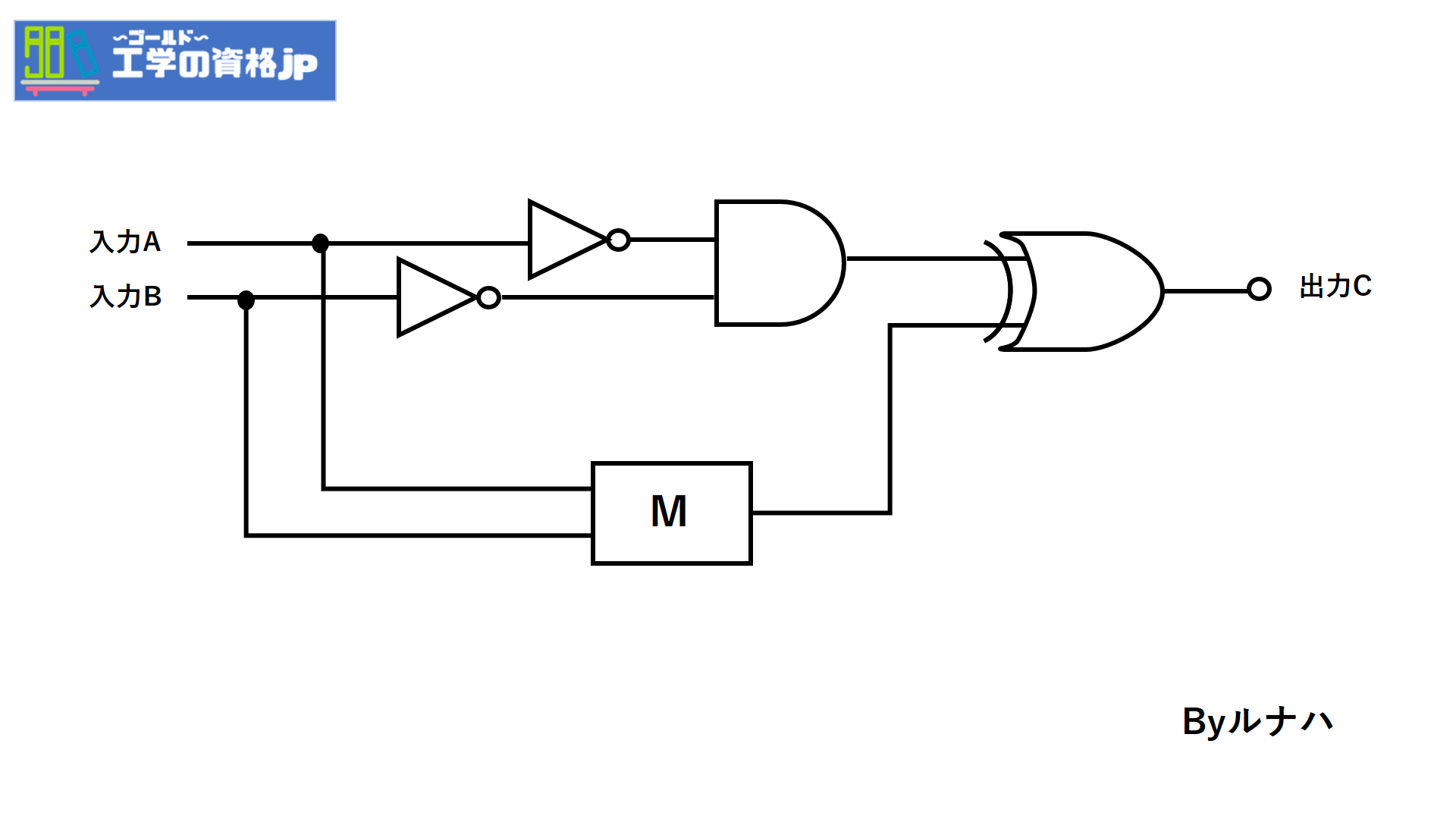
解説
この問題の解説は今回が初めてです。論理回路の中では面倒な部類ですので解説をやってこなかったのですが要望もありやっていきたいと思います。
この問題は論理回路では必ず出ています。
解くコツはそこまでありません。
一つ一つの素子をMの中に入れていき出力Cの論理式を簡略化していく作業をするしかありません。
それでは、論理回路に入れていきましょう。
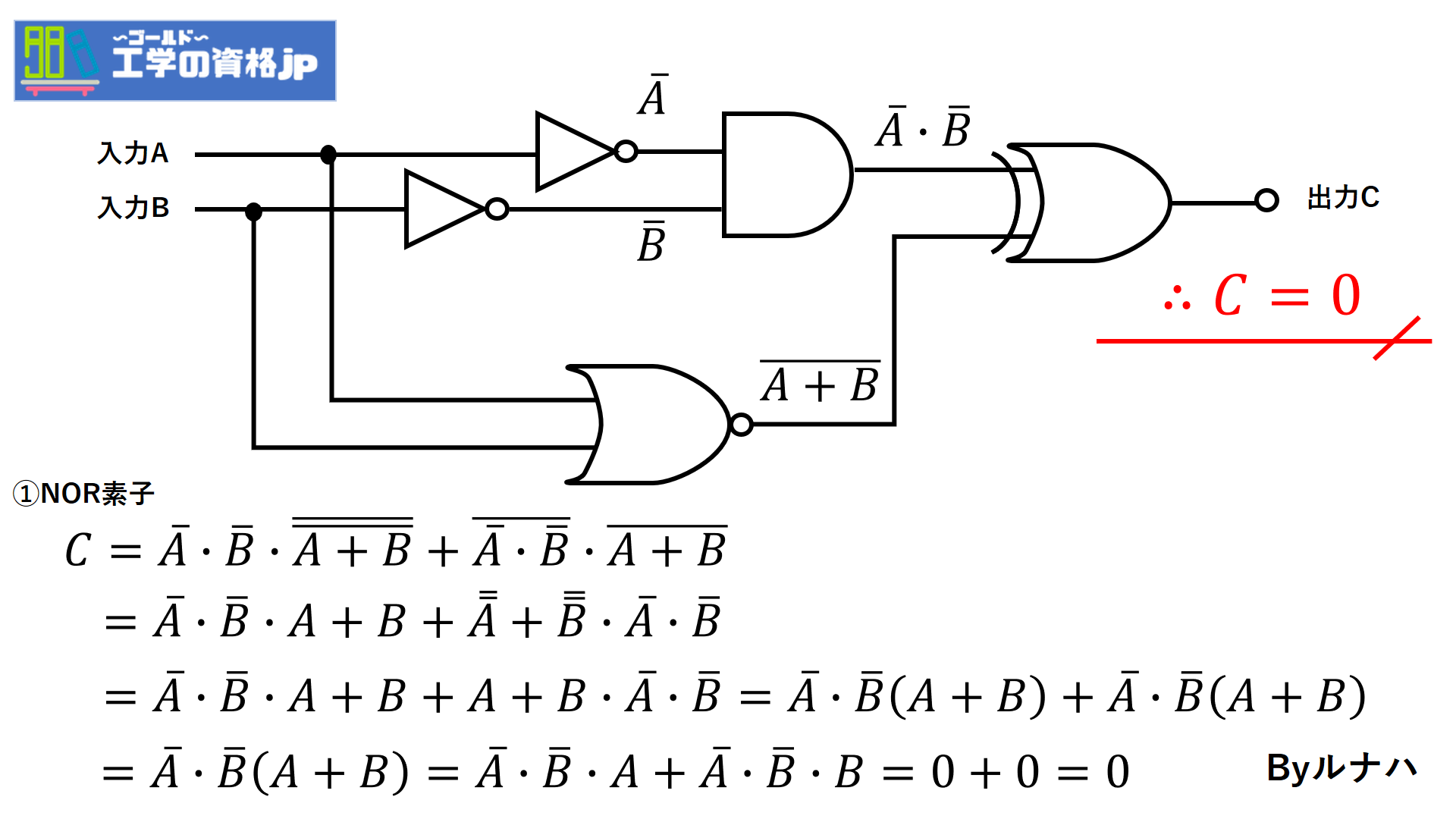
最初は①のNOR素子をMに入れて計算していきます。
次はOR素子です。
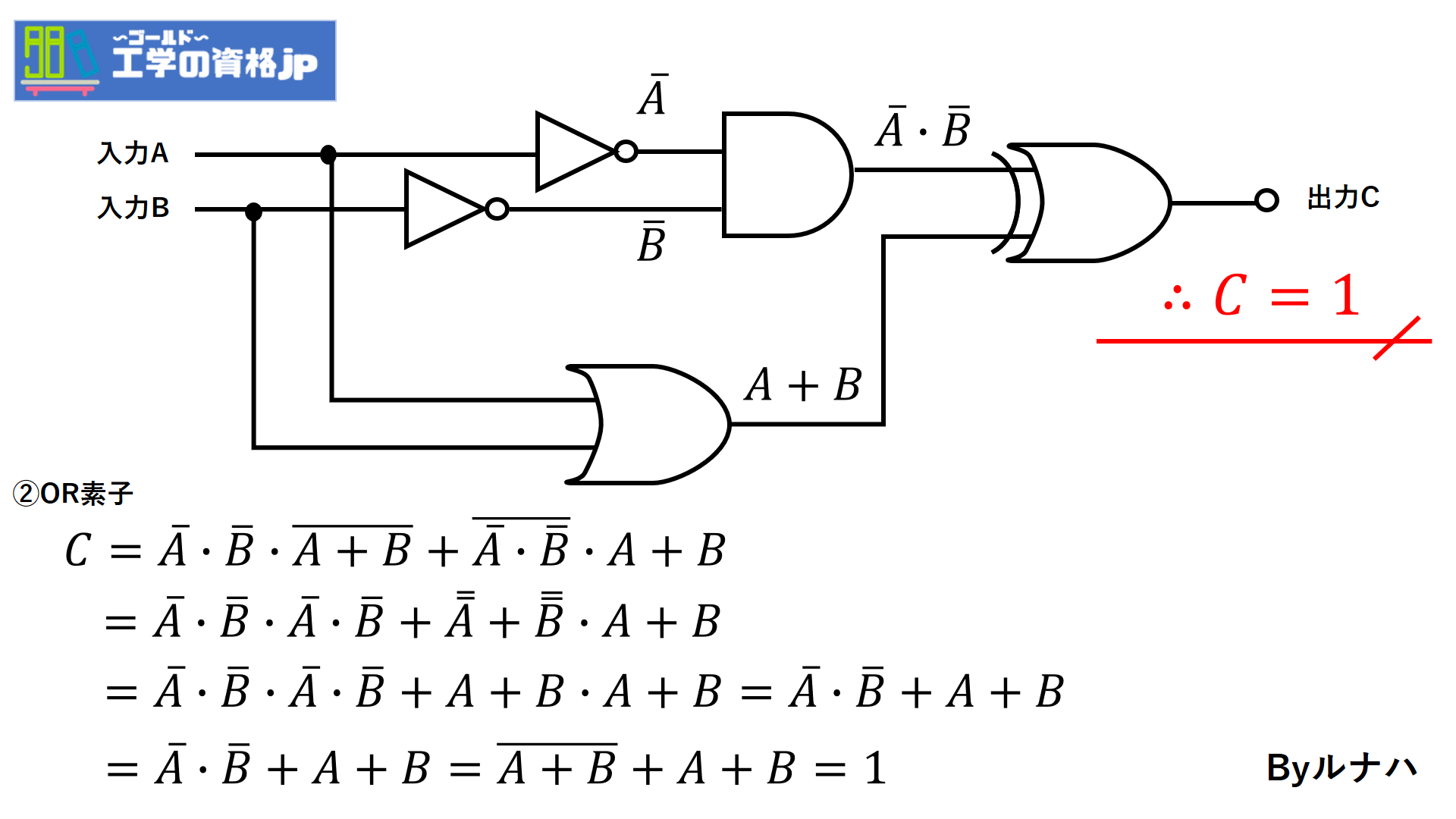
次はNAND素子です。
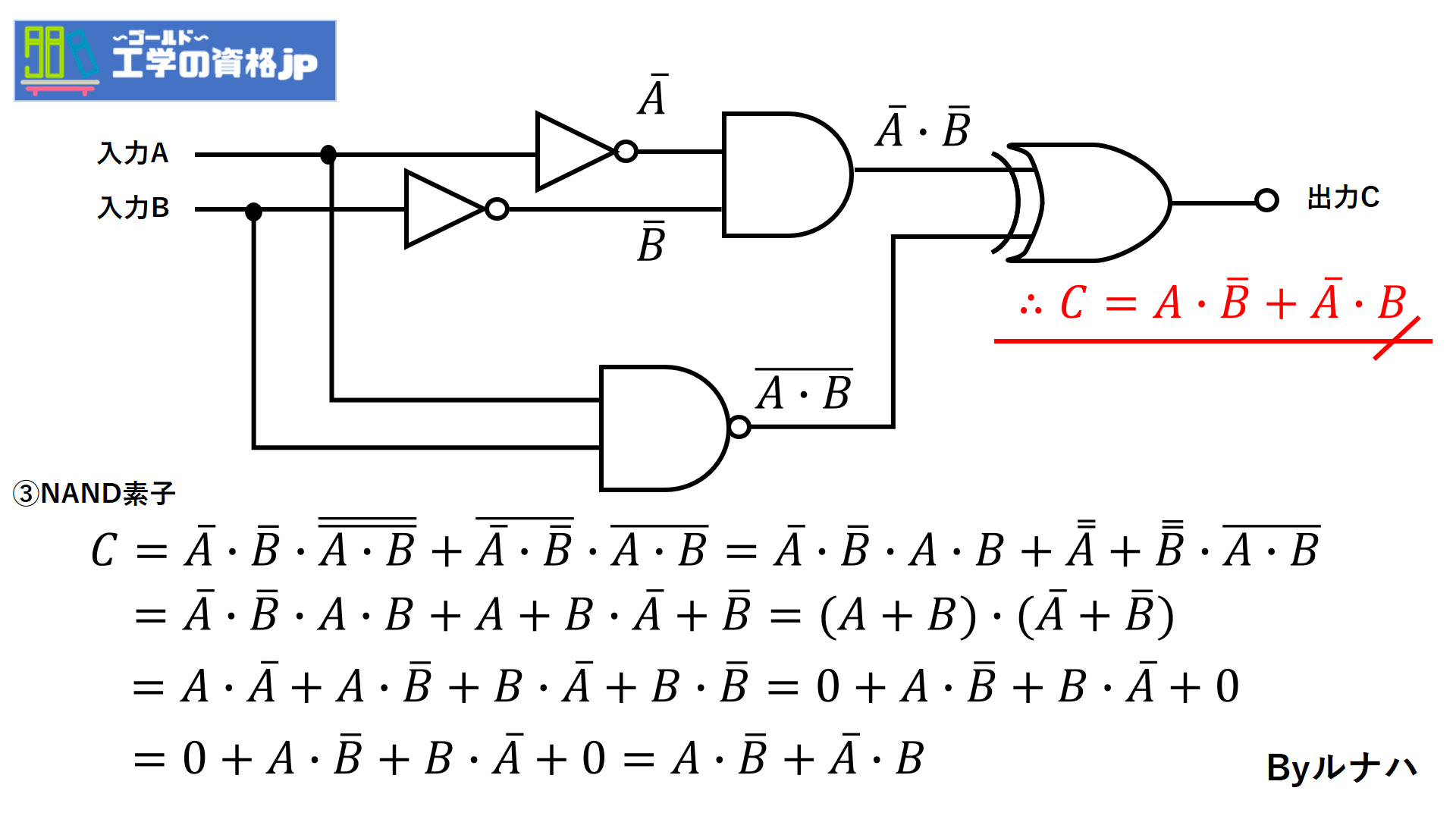
次にAND素子です。
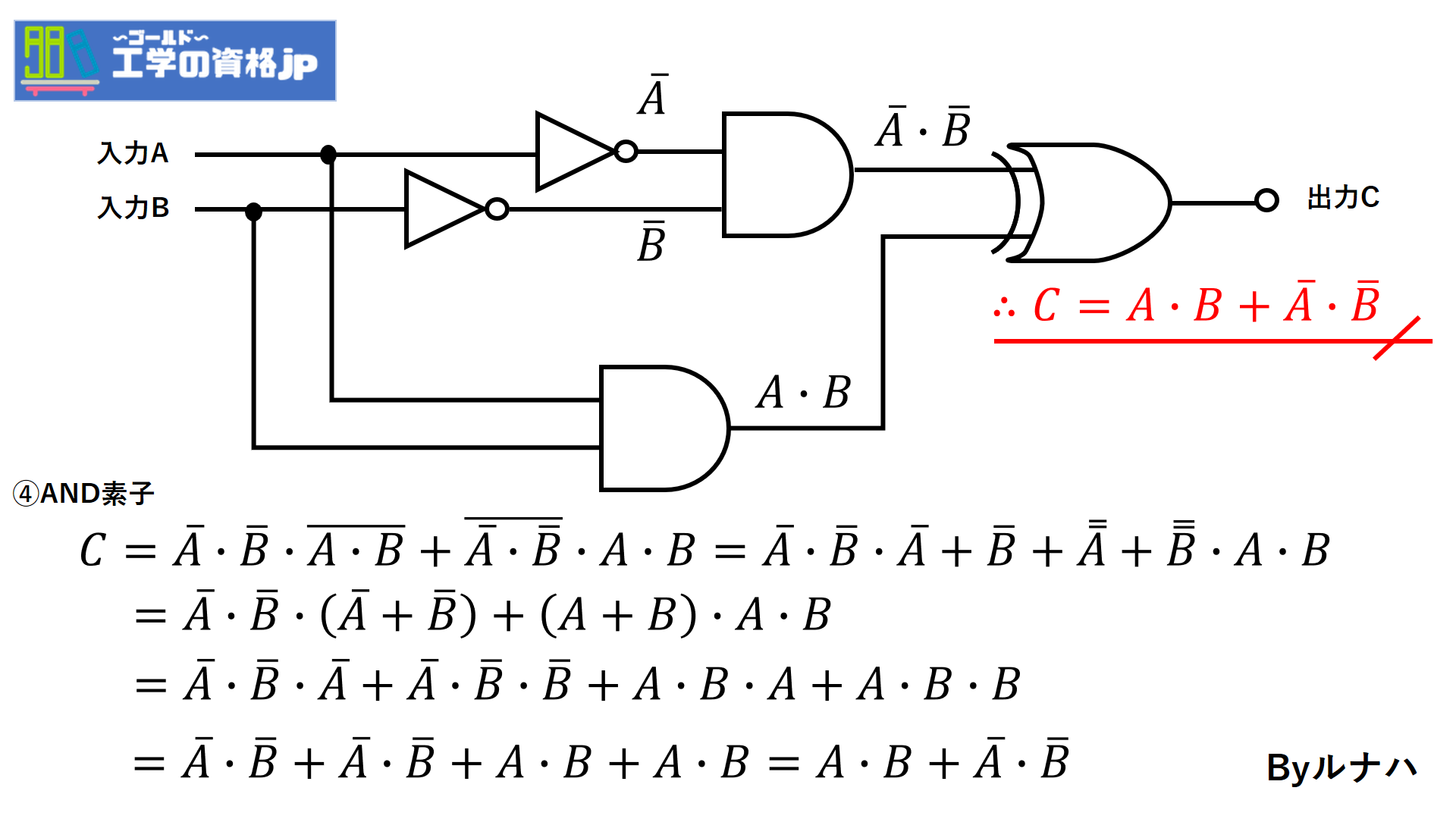
AND素子で問題の出力Cが求まりました。答えはAND素子ですが一応EX-OR素子もやっていきます。
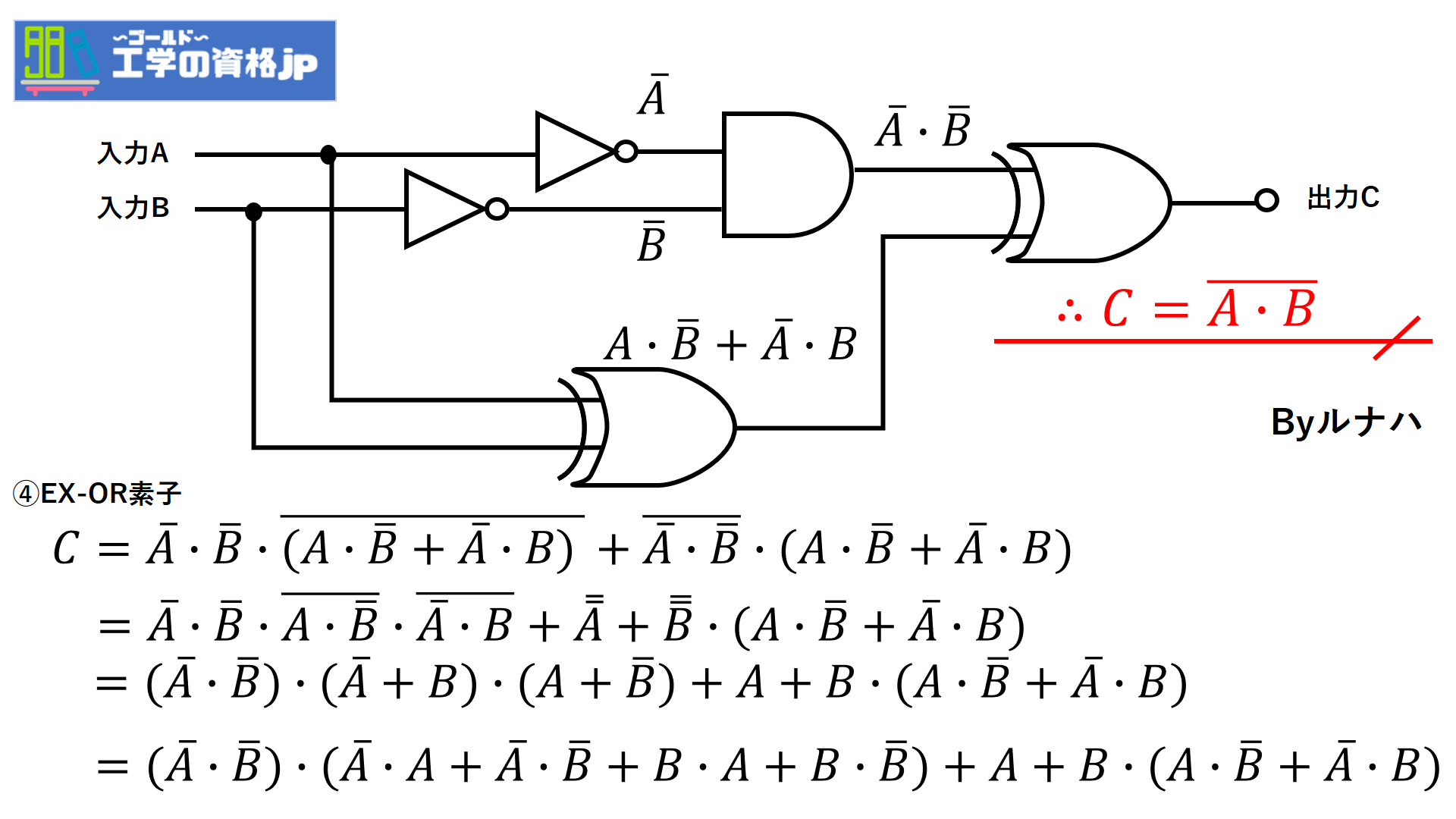
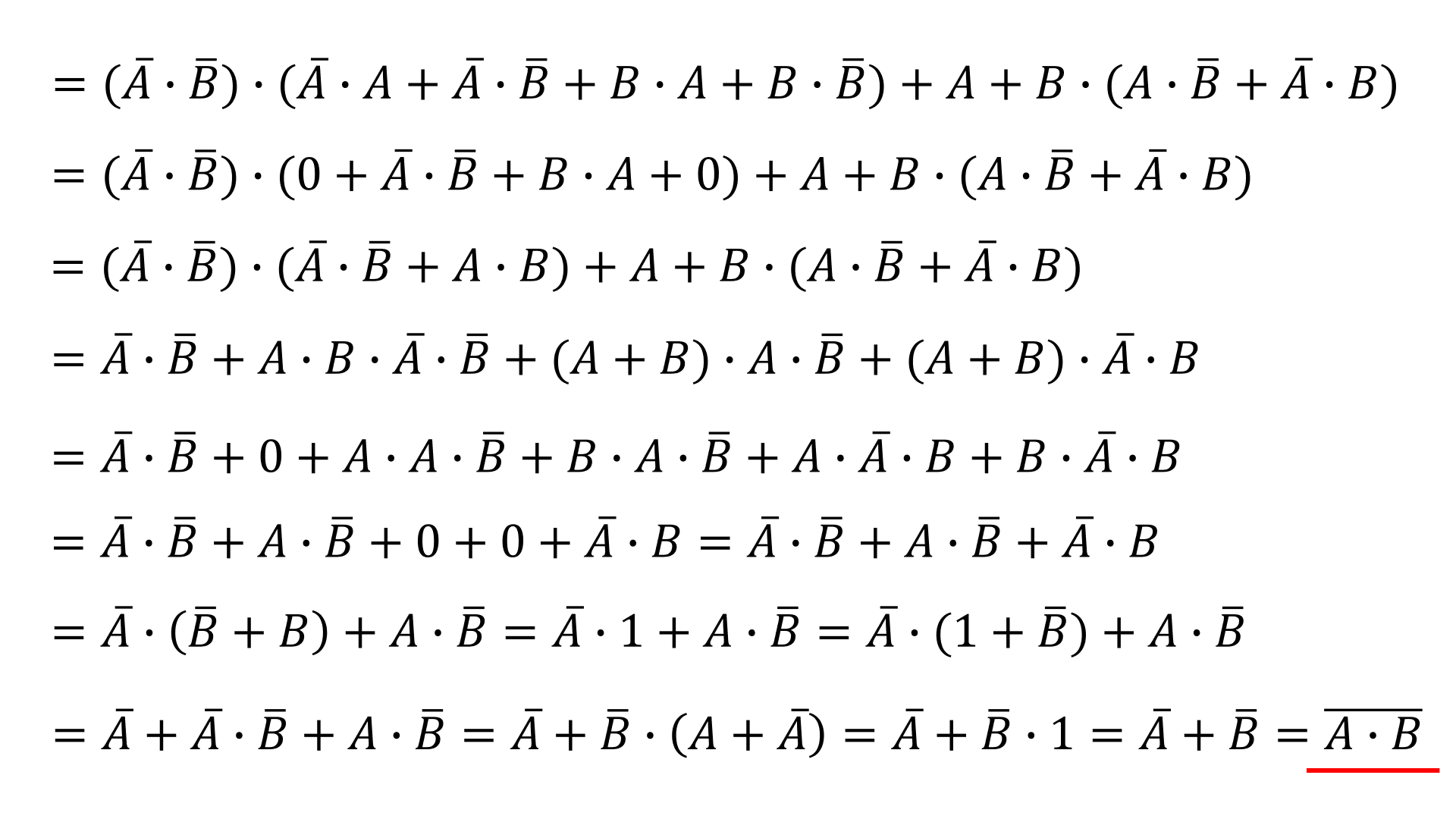
よって答えはANDです。(終)




コメントを残す